Partial fractions vs contour integration

2020 November 19

Unlike differentiation, there is no systematic method for integrating any function given in closed form, but rather a library of calculation techniques (i.e. a calculus) that can be applied ad hoc to specific functions. (Although see also the Risch algorithm for a close miss.)

As a simple example, consider

$\int \frac 1{x^2 + 1}\ dx = \arctan(x)$

which can be solved through various classical techniques, or verified by computing the derivative of $\arctan(x)$ . In fact we’ll find a use for this integral in an upcoming entry. However the integral

$\int_{-\infty}^\infty \frac 1{x^4 + 1}\ dx$

is less obvious, as the corresponding indefinite integral is not easily solvable.

I saw this latter integral presented as an example that is amenable to the use of contour integration methods. However, my lack of familiarity with such method leads me to favor the use of partial fractions for this problem. But when I worked through the problem with partial fractions, it became clear that here the two techniques are really the same in disguise.

Let’s walk through the steps of computing

$I = \int_{-\infty}^\infty \frac 1{P(x)}\ dx$

using both partial fractions and contour integration. Here we take $P(x)$ to be a monic polynomial of degree at least 2, with no repeated roots and no real roots, although in general the following steps equally apply to any quotient of polynomials. Let

$P(x) = (x - r_1) \cdots (x - r_n).$

Partial fractions

We need to find $\alpha_k$ such that

$\frac 1{P(x)} = \frac {\alpha_1}{x - r_1} + \cdots + \frac {\alpha_n}{x - r_n};$

this is called the partial fraction decomposition of $\frac 1P$ . Multiplying both sides by $P(x)$ gives an equality of polynomials in $x$ that needs to hold for all $x$ ; we can regard this as a system of $n$ linear equations with $n$ unknowns. However, the easier way to solve this is to evaluate both sides at $x = r_k$ , as that makes all but one term on the right go to zero. We get

$\alpha_k = \frac 1{P'(r_k)}$

(which you can verify by expanding $P'(x)$ ). These $\alpha$ are the residues of $\frac 1P$ at each of its poles.

Now

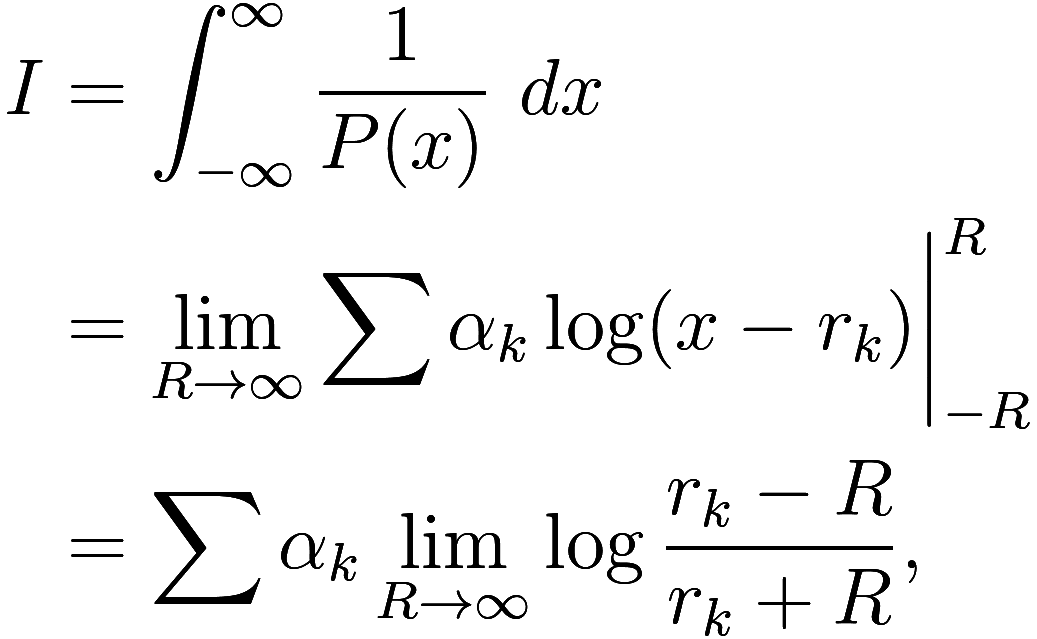
$\begin{aligned} I &= \int_{-\infty}^\infty \frac 1{P(x)}\ dx \\ &= \lim_{R \to \infty} \sum \alpha_k \log (x - r_k) \biggr\rvert_{-R}^R \\ &= \sum \alpha_k \lim_{R \to \infty} \log \frac {r_k - R}{...$

so it remains to calculate the limit of this log expression. As we are taking log of complex numbers, we need to be careful to choose a branch cut of log that is not crossed by the line from $r_k - R$ to $r_k + R$ . The standard choice for the branch cut, the negative real axis, works for this purpose as we have specified that none of the $r_k$ are real. (If any of the $r_k$ are real we would need to deal with integrating through a singularity in $\frac 1P$ .)

We know that

$\log\left(m e^{i\theta}\right) = \log(m) + i \theta$

so we need to know the magnitude $m$ of $\frac {r_k - R}{r_k + R}$ for large $R$ , and its angle $\theta$ . In the limit of large $R$ , its magnitude goes to 1. The angle depends on whether the imaginary part of $r_k$ is positive. If $\Im r_k > 0$ , then the angle of $\frac {r_k - R}{r_k + R}$ approaches $\pi$ ; otherwise $-\pi$ . Thus we have

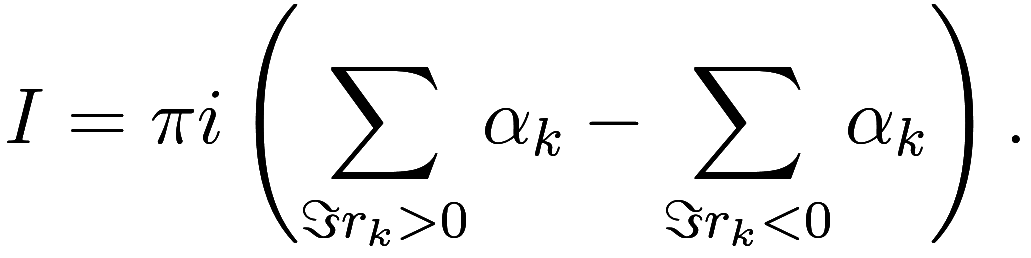
$I = \pi i \left( \sum_{\Im r_k > 0} \alpha_k - \sum_{\Im r_k < 0} \alpha_k \right).$

This can be simplified slightly: let us show that the sum of the residues $\alpha_k$ is zero. In the next section we will see an immediate way to prove this. For now, note that in our equation

$1 = \alpha_1 \frac {P(x)}{x - r_1} + \cdots + \alpha_n \frac {P(x)}{x - r_n}$

that $0$ is the coefficient of the $x^{n - 1}$ term on the left, and $\sum \alpha_k$ is the coefficient of the $x^{n - 1}$ term on the right. Then it follows that

$I = 2 \pi i \sum_{\Im r_k > 0} \alpha_k.$

Contour integration

We can calculate $I$ using the residue theorem, which states that

$\oint f(z)\ dz = 2\pi i \sum \text{Res}(f, z_k)$

where $f$ is a meromorphic function and the sum on the right is of the residues of $f$ at each of the poles inside of the contour. The definition of residue is the unique value such that the difference

$f(z) - \frac {\text{Res}(f, a)}{z - a}$

has an antiderivative in a small punctured disc around $z = a$ . (It is fine if $f$ has a pole of order higher than 2, as integrating $z^n$ only creates a branch cut when $n = -1$ exactly. Thus the residue is the coefficient of the $z^{-1}$ term.)

The residue theorem is a direct consequence of Cauchy’s theorem, which states that the contour integral of a holomorphic function is zero. Suppose we want to use this to compute a contour integral that goes around some poles. Then by Cauchy’s theorem we can write $\oint f(z)\ dz$ as a sum of contour integrals, one for each pole, each of them going in a circle of arbitrarily small radius around that pole. Then, by definition of residue, we can replace these integrals with ones of the form $\frac 1{z - z_k}$ that can be computed easily to give the desired result.

So what are these residues for the function $\frac 1P$ ? Unsurprisingly, the residue of $\frac 1P$ at $r_k$ is $\alpha_k$ , as can be seen from the equation

$\frac 1{P(x)} = \frac {\alpha_1}{x - r_1} + \cdots + \frac {\alpha_n}{x - r_n}$

together with the definition of residue. Then if we choose a contour to integrate around, the residue theorem tells us that

$\oint \frac 1{P(x)}\ dx = 2 \pi i \sum \alpha_k$

where the sum is taken over $\alpha_k$ such that $r_k$ is inside of the contour.

It remains to choose a suitable contour. First, imagine taking a large circle of radius $R$ around the origin, with $R > \max |r_k|$ , and let $J_R = \oint \frac 1{P(x)}\ dx$ be the value of the integral.

In the limit $R \to \infty$ , the length of the path being integrated along grows like $R$ , but the integrand $\frac 1P$ shrinks like $R^{-\deg P} \leq R^{-2}$ , so $\lim J_R \to 0$ . But by the residue theorem, $J_R$ only depends on which poles are inside the contour, which is independent of $R$ , so $J_R = 0$ . Therefore

$0 = 2 \pi i \sum \alpha_k$

where the sum on the right is over all $\alpha_k$ . This gives us again our result that the residues have a sum of zero, which we needed in the previous section.

Now we return to computing $I$ and choose a semicircular contour, running along the real axis from $-R$ to $R$ , and then following a semicircular arc in the upper-half plane; let $I_R$ be the value of this integral.

$I_R$ is a sum of two components, for the two parts of the path being integrated along. As with $J_R$ , the semicircular arc component goes to 0 in the limit of large $R$ . And again as before, the value of $I_R$ is independent of $R$ for large $R$ , so

$I = \lim_{R \to \infty} \int_{-R}^R \frac 1{P(x)}\ dx = \lim_{R \to \infty} I_R = I_R.$

Then we compute $I_R$ with the residue theorem, giving

$I = 2 \pi i \sum_{\Im r_k > 0} \alpha_k,$

where the sum is over roots $r_k$ in the upper-half plane, in agreement with the result of the computation with partial fractions.

Discussion

Step-by-step, the two methods involve nearly the same operations. With contour integration, we took advantage of Cauchy’s theorem and that $\frac 1P$ is holomorphic to choose contours that are convenient instead of being committed to integrating along the real axis. This made it trivial to find the sum of the residues, and also simplified the task of integrating the functions $\frac 1{x - r_k}$ . When integrating along the real axis, we had to do some geometric reasoning about whether the imaginary part of $r_k$ is positive or negative, but using Cauchy’s theorem we can instead integrate in a circle around $r_k$ , which was elided as “easy” in our sketch of the proof of the residue theorem.

Otherwise, the two methods are identical. I was surprised that to calculate the residues by directly applying the definition of “residue” as given on Wikipedia requires first finding the partial fraction decomposition. Of course, while there are various theorems that hasten the calculation of the residues in practice, these are equally applicable to hastening the partial fraction decomposition.

Let us work through the specific example $P(x) = x^{2n} + 1$ . If $\zeta$ is the primitive $4n$ th root of unity $e^{2\pi / 4n}$ , then the roots of $P$ are

$r_k = \zeta^{2k - 1}$

for $k= 1, \ldots, 2n$ , of which the first $n$ have positive imaginary part. As $P'(x) = 2n x^{2n - 1}$ , we get

$\alpha_k = \frac 1{P'(r_k)} = \frac 1{2n} \zeta^{-(2k - 1)(2n - 1)} = \frac 1{2n} \zeta^{2n - 1} \zeta^{2k},$

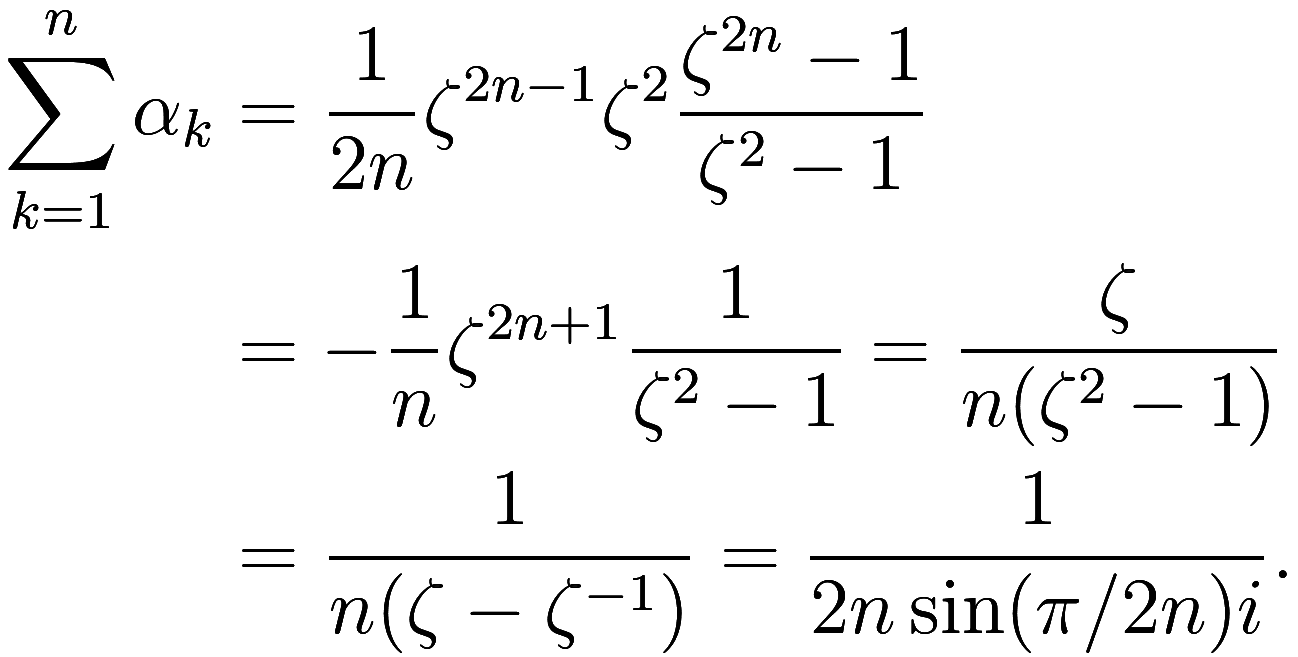
$\begin{aligned} \sum_{k = 1}^n \alpha_k &= \frac 1{2n} \zeta^{2n - 1} \zeta^2 \frac{\zeta^{2n} - 1}{\zeta^2 - 1} \\ &= -\frac 1n \zeta^{2n + 1} \frac 1{\zeta^2 - 1} = \frac \zeta {n(\zeta^2 - 1)} \...$

Finally we get

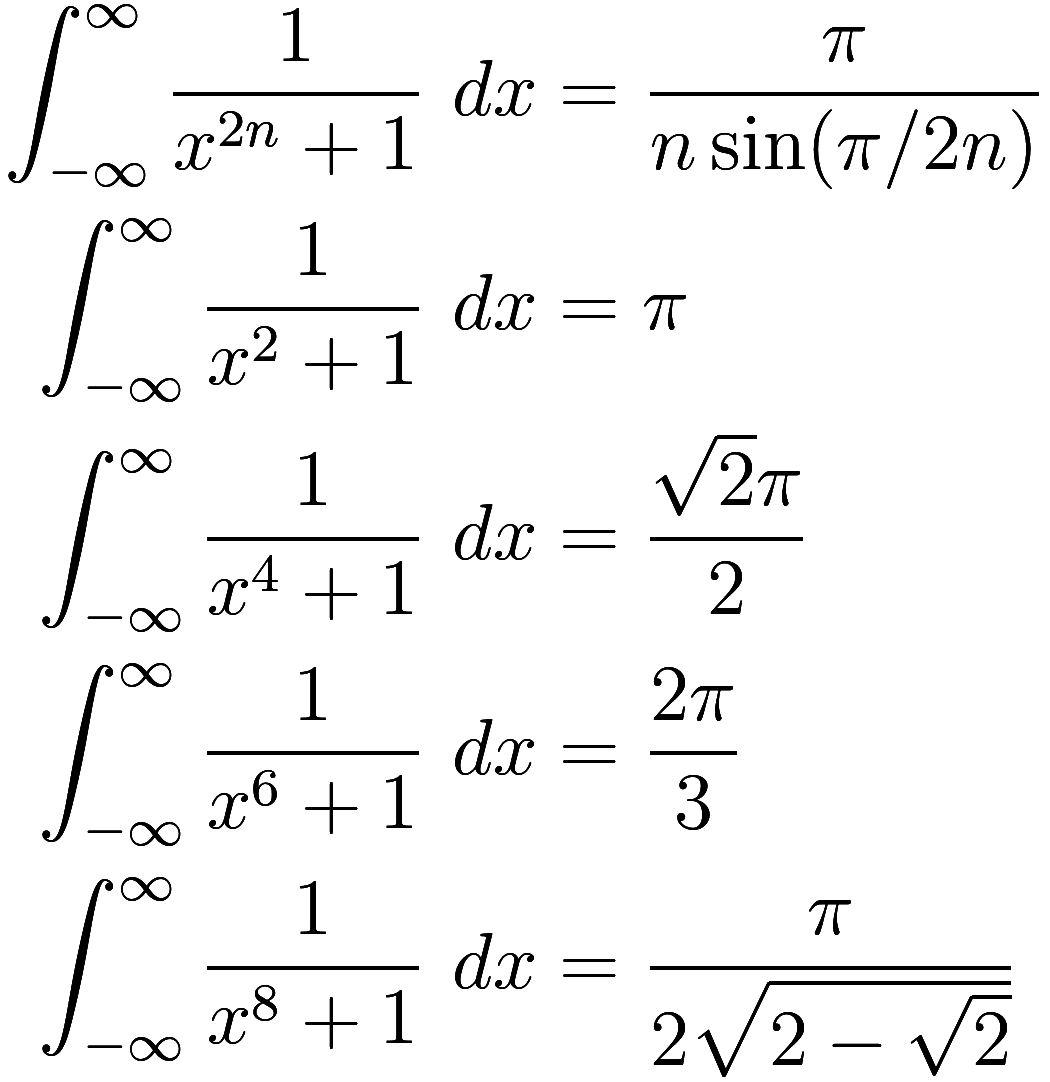
$\begin{aligned} \int_{-\infty}^\infty \frac 1{x^{2n} + 1}\ dx &= \frac \pi {n \sin(\pi / 2n)} \\ \int_{-\infty}^\infty \frac 1{x^2 + 1}\ dx &= \pi \\ \int_{-\infty}^\infty \frac 1{x^4 + 1}\ dx &= \...$

Follow RSS/Atom feed for updates.