What is gravitoelectromagnetism?

2021 May 08

In Newtonian gravity, the acceleration towards a massive particle with mass $M$ and distance $d$ is

$\frac M {d^2}$

times some constant. What happens if the particle is moving? We know from relativity that information cannot travel faster than the speed of light $c$ , so any movements of the particle in the last $d / c$ time cannot influence the current gravitational acceleration.

One might guess that a test particle is simply accelerated towards where the massive particle was $d / c$ ago. However, in relativity, it is impossible to measure your absolute velocity – only the relative velocity between particles is observable. Therefore if the test and massive particles are moving at the same velocity, then the acceleration must be directly towards where the massive particle is and not towards where it was, in contradiction to our guess.

Reality is more complicated, and we find that the gravitational force depends on the velocities of the particles. This is analogous to electromagnetism: while both the electric and magnetic forces were discovered before relativity, with the discovery of relativity it was realized that the magnetic force is simply the velocity-dependent component of the electric force.

One observable consequence of the gravity’s velocity-dependence is frame-dragging, in which a rotating massive object causes nearby objects to counter-rotate.

Assuming that gravity, like electromagnetism, is Lorentz invariant we can work out the full non-static gravitational equations – although see the caveat at the end. The resulting theory is called gravitoelectromagnetism, and was suggested in 1893 by Oliver Heaviside.

Maxwell’s equations for electromagnetism are

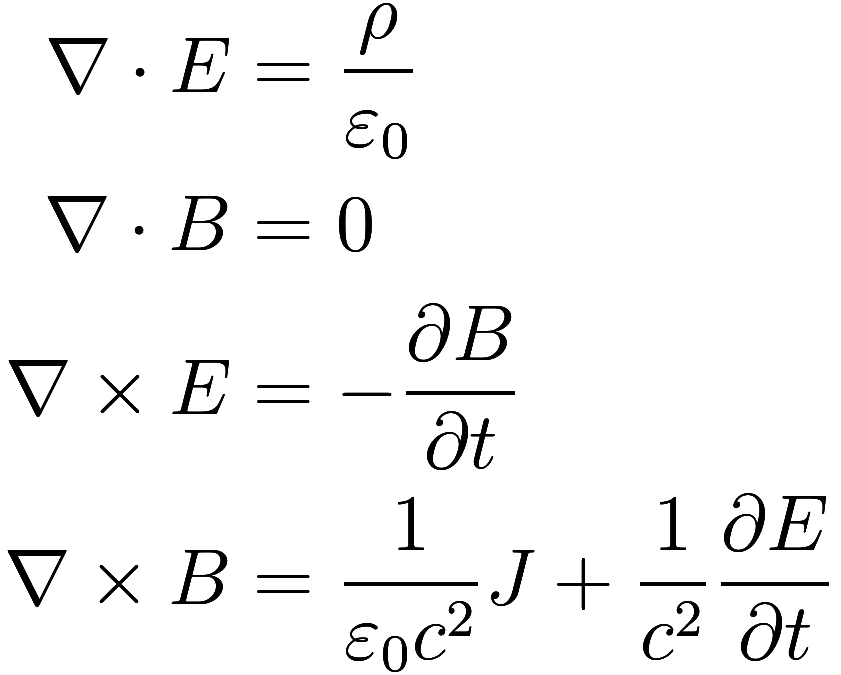
$\begin{aligned} \nabla \cdot E &= \frac {\rho}{\varepsilon_0} \\ \nabla \cdot B &= 0 \\ \nabla \times E &= - \frac {\partial B}{\partial t} \\ \nabla \times B &= \frac 1{\varepsilo...$

where $E$ and $B$ are the electric and magnetic fields, $\rho$ is the charge density, and $J$ is the charge flux; the other terms being physical constants.

Then the equations for gravitoelectromagnetism are almost identical:

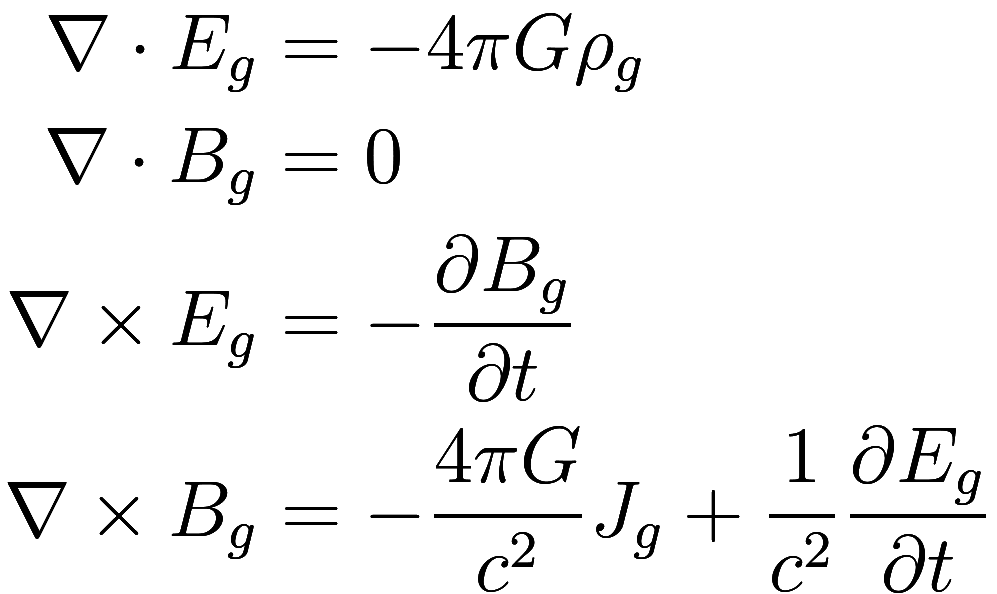
$\begin{aligned} \nabla \cdot E_g &= -4 \pi G \rho_g \\ \nabla \cdot B_g &= 0 \\ \nabla \times E_g &= - \frac {\partial B_g}{\partial t} \\ \nabla \times B_g &= - \frac {4 \pi G}{c^...$

Here $\rho_g$ is mass density, $J_g$ is mass flux, and $E_g$ is the “gravitoelectric” field (i.e., the conventional gravitational field) and $B_g$ the “gravitomagnetic” field (i.e., the velocity-dependent component).

These equations show how the electromagnetic fields $E, B$ and gravitoelectromagnetic fields $E_g, B_g$ are defined by a distribution of charges ( $\rho$ or $\rho_g$ ) and their velocities ( $J$ or $J_g$ ). Having defined the fields, the force exerted on a slow test particle of charge $q$ or mass $m$ and velocity $v$ is

$\begin{aligned} F &= q(E + v \times B) \\ F_g &= m(E_g + v \times 4B_g) \end{aligned}$

After adjusting constants, the electromagnetic equations and gravitoelectromagnetic equations are almost the same as each other: the factor of 4 in the gravitomagnetic force does not go away. This may seem unimportant, but in fact arises from differences in the fundamental nature of gravity and electromagnetism, and has a crucial impact in the usefulness of gravitoelectromagnetism as a theory. (Heaviside’s 1893 formulation omits the $B_g$ contribution to force entirely.) Recall of course that gravitoelectromagnetism is only an approximation of general relativity, which gives a fully accurate theory of gravity. When performing this approximation, the factor of 4 inevitably arises. While general relativity is rather beyond me and I have only the dimmest understanding of why there is a 4, I will present what I believe the root cause to be.

In special relativity, Maxwell’s equations can be condensed into a single equation

$\partial_\alpha F^{\alpha \beta} = \mu_0 J^\beta$

where $F^{\alpha \beta}$ is the electromagnetic tensor and contains all the information of the electric and magnetic fields $E$ and $B$ , and $J^\beta$ is the four current, which has four dimensions. The time-like component of the four current is the charge $\rho$ , and the space-like coordinates are the charge flux:

$J = (\rho, J^1, J^2, J^3)$

In contrast, in general relativity the source of gravity is the stress-energy tensor (“tensor” is physicist-speak for a matrix, and a distant relative of the mathematical notion of tensor). The time-time component of the stress-energy tensor is the mass density $\rho_g$ , the time-space components are the momentum density, and the space-space components are the momentum flux:

$T = \begin{pmatrix} \rho_g & p^1 & p^2 & p^3 \\ p^1 & T^{11} & T^{12} & T^{13} \\ p^2 & T^{21} & T^{22} & T^{23} \\ p^3 & T^{31} & T^{32} & T^{33} \end{pmatrix}$

The momentum flux is the “stress” part of the stress-energy tensor, with the diagonal components being the pressure, and the off-diagonal components being the shear stress. These stress terms have no analogue in electromagnetism, so if we ignore them we are left with

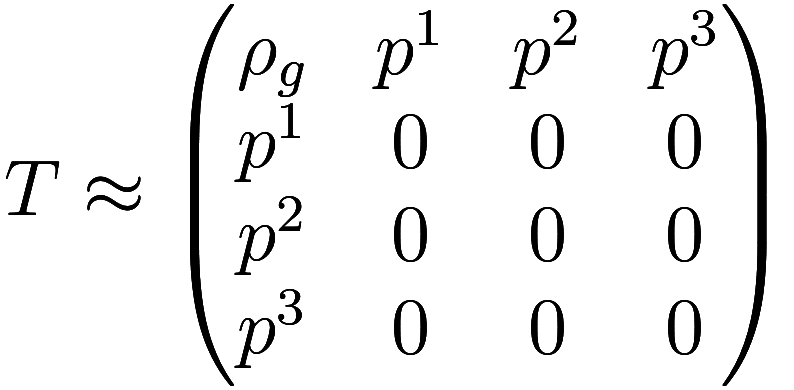
$T \approx \begin{pmatrix} \rho_g & p^1 & p^2 & p^3 \\ p^1 & 0 & 0 & 0 \\ p^2 & 0 & 0 & 0 \\ p^3 & 0 & 0 & 0 \end{pmatrix}$

The momentum terms, which are labelled $p^\alpha$ here, become the gravitomagnetic terms $J_g$ in gravitomagnetism. However, unlike in actual electromagnetism, there are two copies of each of these terms. As a consequence, a particle with gravitoelectric charge (i.e., mass) $m$ will effectively have a gravitomagnetic charge of $2m$ . Since the strength of the gravitomagnetic force is proportional to the product of the gravitomagnetic charges of the particles involved, and both of those charges are doubled, the gravitomagnetic force is 4 times stronger than the analogous magnetic force.

(This above explanation could well be wrong, it was the best I was able to infer from staring at the linked wikipedia articles.)

This distinction between electromagnetism and gravity is sometimes described by calling the electromagnetic field spin 1, meaning it is a vector field with $4^1$ components, and the stress-energy tensor field spin 2, meaning it is a tensor field with $4^2$ components.

Note a critical consequence of arbitrarily zero’ing out the stress terms in $T$ : the resulting tensor field is no longer Lorentzian, so gravitoelectromagnetism is not invariant under Lorentz transformations. The choice of which terms in $T$ are zero’d out depends on which inertial frame we measure the coordinates in – changing frames causes the terms to mix with each other. This result somewhat defeats our initial purpose in introducing gravitomagnetic terms to salvage Newtonian gravity from being non-Lorentzian. Arguably it is even “less” Lorentzian than Newtonian gravity, as 4 is further from 1 than 0. We could achieve true Lorentz invariance by replacing the factor of 4 with 1 in the gravitomagnetic force, but at the cost of no longer approximating the true gravitational force anymore.

Follow RSS/Atom feed for updates.