Cornu spiral and other fractal spirals

2023 February 10

Recently I have been examining discretizations of the Cornu spiral (or Euler spiral or clothoid), which have a remarkable self-similar fractal property. While this analysis of the discrete Cornu spiral is still in progress, it felt incomplete without first considering that the continuous Cornu spiral itself is fractal.

Unlike the better known logarithmic spiral¹which I know as the geometric spiral but apparently this is not a standard name. The logarithmic spiral is often the most natural spiral. or Archimedean spiral²or arithmetic spiral, the Cornu spiral is described by starting a finite distance out of the spiral and then spiraling inwards. The defining property is the curvature varies linearly with the arc length from the starting point; going in either direction, then, yields a double-ended spiral. Thus the coordinates of the spiral are given by the Fresnel integral

$\int_0^L e^{is^2}\ ds$

which has no closed form solution. Integrating to infinity gives a finite value, the center point of the spiral. In contrast to the logarithmic or Archimedean spirals which only have finite arc length in a bounded region, and so are necessarily one-dimensional, the cornu spiral has infinite arc length and could be potentially any fractal dimension from 1 to 2.

Cornu spiral

Let us thus compute the Minkowski or box-counting dimension of the cornu spiral. To do this, for a length $\ell$ we count how many $N(\ell)$ squares of side-length $\ell$ it takes to cover the whole cornu spiral. For a $d$ -dimensional figure we expect

$N(\ell) \sim \frac {A}{\ell^d}$

(where $A$ is a $d$ -dimensional “area”) and thus define the Minkowski dimension as

$d = -\lim_{\ell \to 0} \frac {\log(N(\ell))}{\log(\ell)}.$

In the normalized cornu spiral, the radius of curvature $R$ at an arc length $L$ is given by

$2RL = 1,$

as $R$ is the inverse of the curvature and curvature goes linearly with length. When $L$ is very large the spiral approximates a circle of radius $R = 1 / 2L$ around the center point. After an additional rotation around the center, our new arc length is $L + 2\pi R$ , and so the new radius of curvature is

$R' = \frac 1{2L'} = \frac 1{2(L + 2\pi R)} = \frac 1{2(1 / 2R + 2\pi R)} = \frac R{1 + 4\pi R^2}.$

So, the gap between one spiral turn and the next is

$R - R' = R - \frac R{1 + 4\pi R^2} = \frac {4 \pi R^3}{1 + 4\pi R^2} \approx 4 \pi R^3.$

This alternatively could be found using derivatives:

$-2\pi R \frac {dR}{dL} = (2 \pi R) (1 / 2L^2) = (2 \pi R) (2 R^2) = 4\pi R^3.$

Now we know enough about the shape of the spiral to count how many boxes $N$ are needed to cover it. Say the boxes are squares with side length $\ell$ . Then within some critical radius $R^*$ boxes from consecutive turns start to overlap, and it is best to just cover the whole circle with $\pi (R^*)^2 / \ell^2$ boxes. Note that $\ell = 4 \pi (R^*)^3$ , the gap between one spiral turn and the next at the critical radius $R^*$ .

Outside of this critical radius the number of boxes is simply the length $L^* = 1 / 2R^*$ of the curve divided by the width $\ell$ of each box. Thus the total number of boxes is:³This is an approximation – after all, it is not an integer – but the error term goes to zero as $R^* \to 0$ , and even if the error term did not go to zero, a constant factor on the number of boxes has no effect on the fractal dimension.

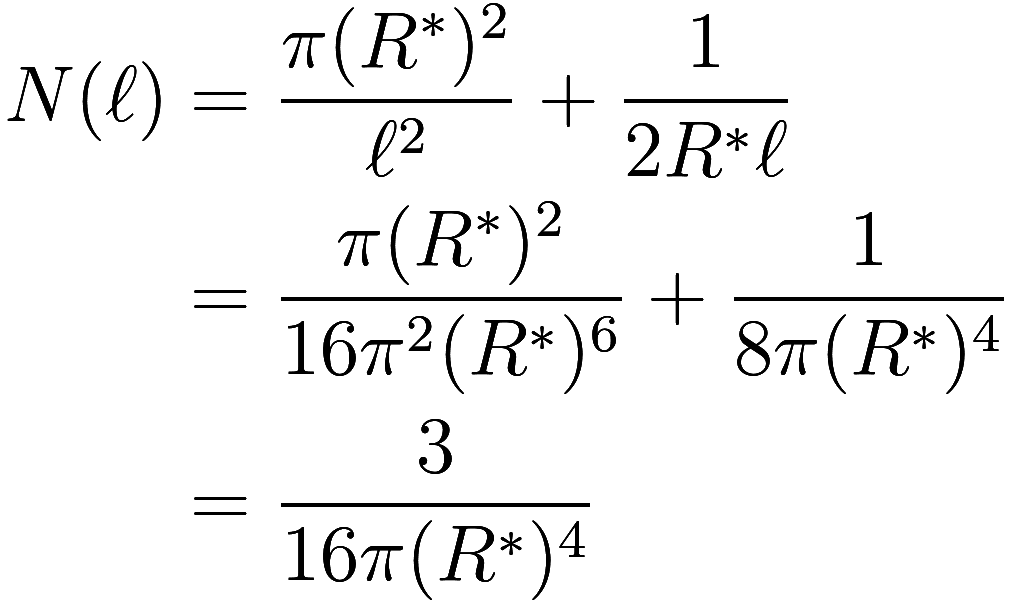
$\begin{aligned} N(\ell) &= \frac {\pi (R^*)^2}{\ell^2} + \frac 1{2R^*\ell} \\ &= \frac {\pi (R^*)^2}{16 \pi^2 (R^*)^6} + \frac 1{8 \pi (R^*)^4} \\ &= \frac {3}{16 \pi (R^*)^4} \end...$

Curiously we find that one-third of the boxes needed to cover the spiral are within the radius $R^*$ , and two-thirds are outside of that radius.

Therefore the Minkowksi fractal dimension is 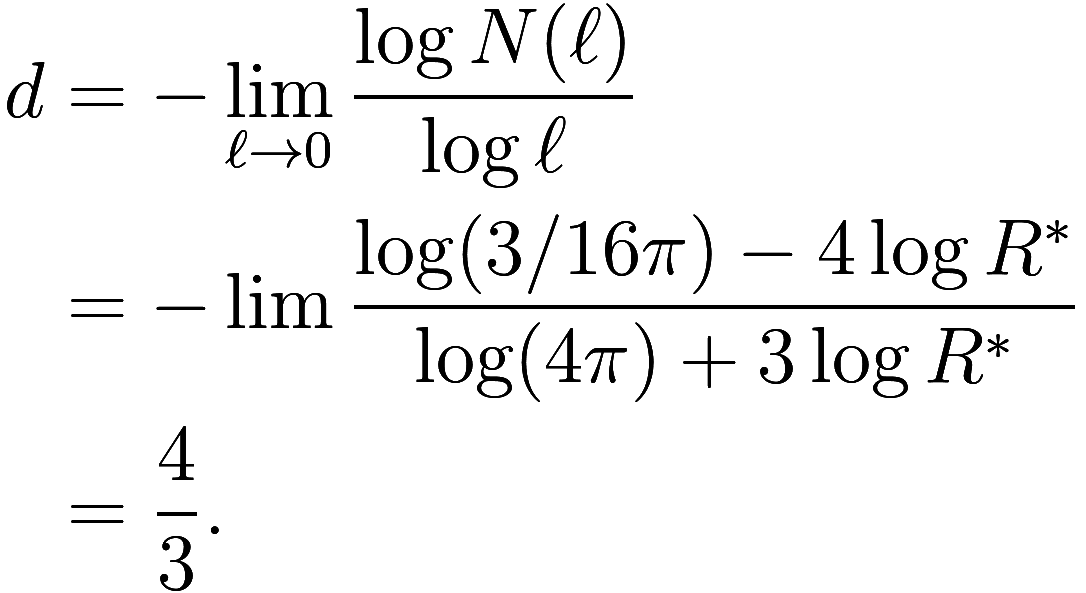$\begin{aligned} d &= -\lim_{\ell \to 0} \frac {\log N(\ell)}{\log \ell} \\ &= -\lim \frac {\log(3 / 16\pi) - 4 \log R^*}{\log(4\pi) + 3 \log R^*} \\ &= \frac 43. \end{aligned}$

Power-law spirals

We can generalize this result, and consider similar “power law” spirals. Suppose that we have a spiral such that, at a radius of $R$ from the center, the gap between consecutive turns scales like $R^\alpha$ ; for the cornu spiral we had $\alpha = 3$ . The logarithmic spiral satisfies $\alpha = 1$ , and the Archimedean spiral has $\alpha = 0$ . The total length of the spiral from $R_0$ to $R_1$ is approximately⁴We are supposing that the spiral is always tangent to a circle centered at the spiral center, which is not correct.

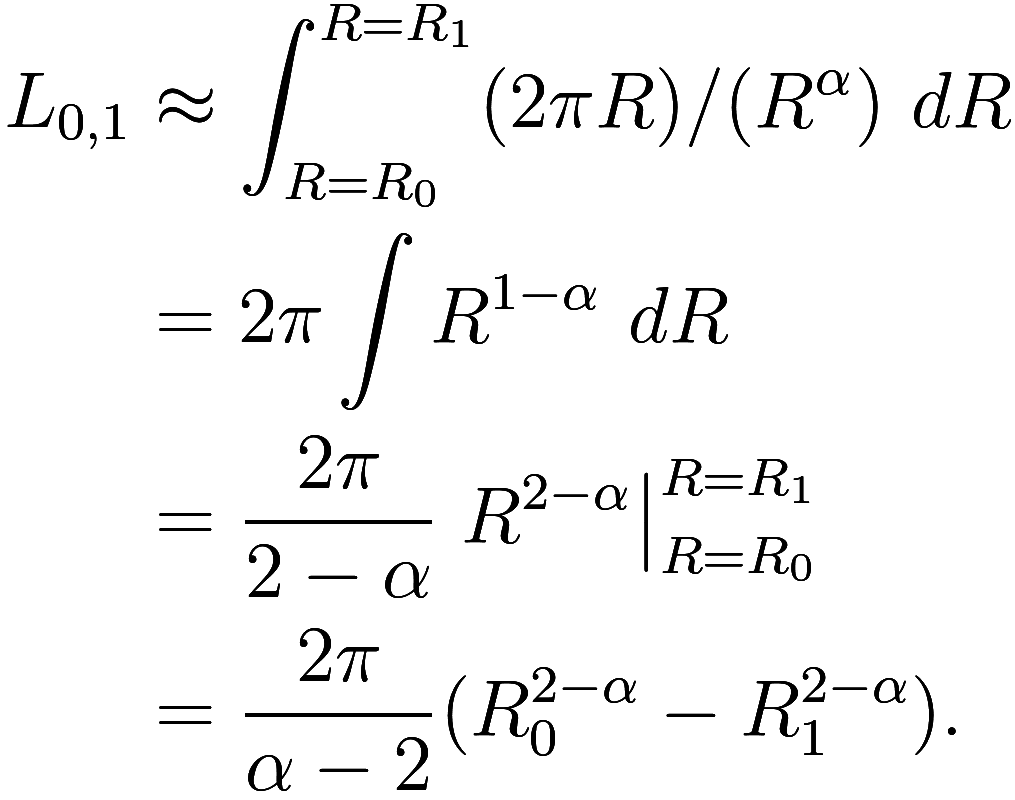
$\begin{aligned} L_{0, 1} &\approx \int_{R = R_0}^{R = R_1} (2\pi R) / (R^\alpha)\ dR \\ &= 2 \pi \int R^{1 - \alpha}\ dR \\ &= \frac {2 \pi}{2 - \alpha} \left. R^{2 - \alpha} \right\rv...$

where $\alpha \neq 2$ . Whoops – this approximation is not always great: for $\alpha < 1$ , it is problematic when $R_0 \to 0$ , and for $\alpha > 1$ when $R_1 \to \infty$ , as in those cases the spiral becomes quite steep. At $\alpha = 1$ it is simply off by a constant term that does not depend on $R$ . So, being more careful we find

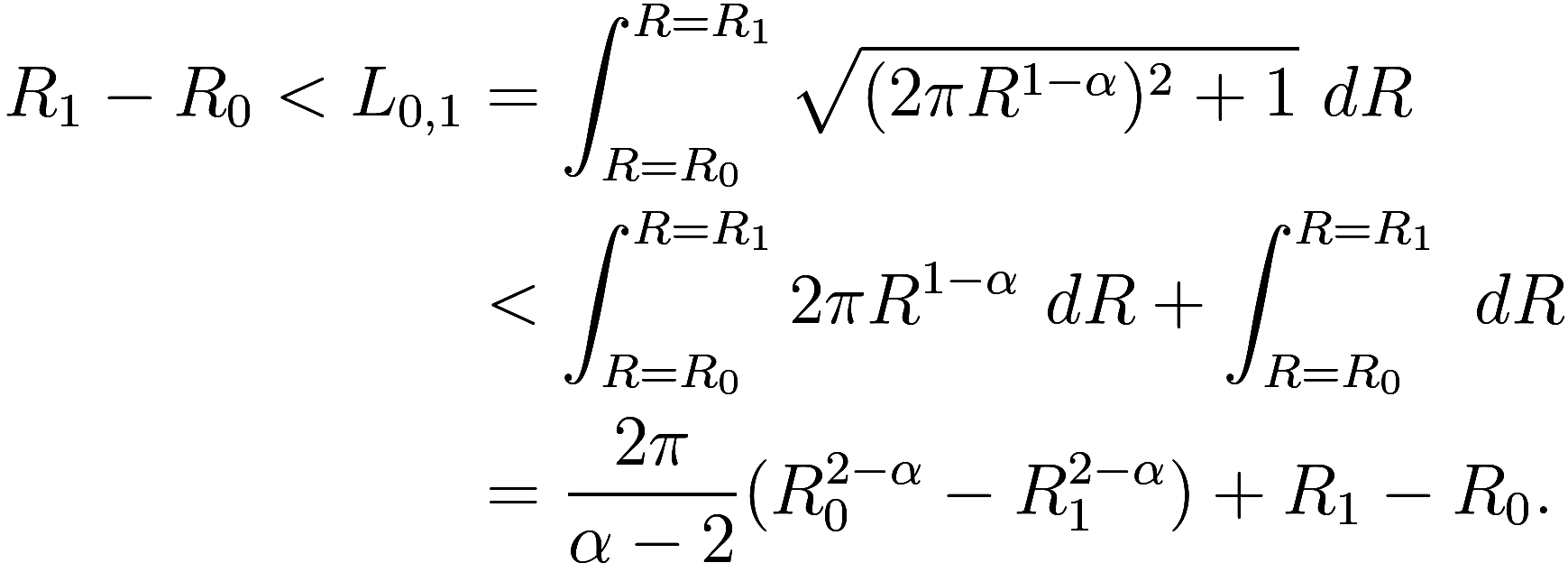
$\begin{aligned} R_1 - R_0 < L_{0, 1} &= \int_{R = R_0}^{R = R_1} \sqrt{(2\pi R^{1 - \alpha})^2 + 1}\ dR \\ &< \int_{R = R_0}^{R = R_1} 2\pi R^{1 - \alpha}\ dR + \int_{R = R_0}^{R = R_1}\ d...$

where again $\alpha \neq 2$ . For $\alpha = 2$ we have instead $R_1 - R_0 < L_{0, 1} < 2 \pi (\log R_1 - \log R_0) + R_1 - R_0.$

We see that for $\alpha < 2$ the spiral has finite length as $R_0 \to 0$ , and so it is not a fractal and has dimension 1. Only for $\alpha \geq 2$ do we have a fractal.

Now we proceed as before, covering the spiral with boxes of size $\ell$ such that within a critical radius $R^*$ the whole circle is covered with no gaps, and $\ell = (R^*)^\alpha$ . We fix some outer radius $R_1$ . Then the number of boxes is

$\begin{aligned} N(\ell) &\approx \frac {\pi (R^*)^2}{\ell^2} + \frac {2 \pi}{\alpha - 2} ((R^*)^{2 - \alpha} - R_1^{2 - \alpha}) / \ell \\ &= \pi (R^*)^{2 - 2\alpha} + \frac{2 \pi}{\alpha ...$

Therefore the Minkowksi fractal dimension is $2 - 2 / \alpha$ . Here we neglected the error term in the integral for $L_{0, 1}$ as it is small for $\alpha \geq 2$ in the limit $R_0 \to 0$ . If $\alpha = 2$ , we instead find

$N(\ell) \sim - (\log R^*) (R^*)^{-2} \sim - (\log \ell) \ell^{-1}$

so while the length of the spiral is infinite the fractal dimension is still only 1!

Follow RSS/Atom feed for updates.