Why poll accuracy does not depend on population size

2020 May 28

A common source of confusion about polls is that poll accuracy depends on the number of people who answered the poll (larger polls are more accurate) but does not depend on population size: a poll of 1000 people in Nebraska has the same error about the typical Nebraskan as a poll of 1000 Americans has for the typical American.

Let’s carefully set up the scenario we are considering. Suppose some unknown proportion $p$ of a population answers “yes” to a yes/no question of interest, and we randomly sample $N$ people from this population and determine their responses. We calculate what fraction $\overline p$ of the responses were yes, and use $\overline p$ as an estimate for $p$ : hopefully $\overline p$ is near the correct value $p$ . While we don’t know the true error $\overline p - p$ , as we don’t know $p$ , a common way of describing the typical error is with the standard deviation $\sigma$ of $\overline p$ , which in our scenario equals

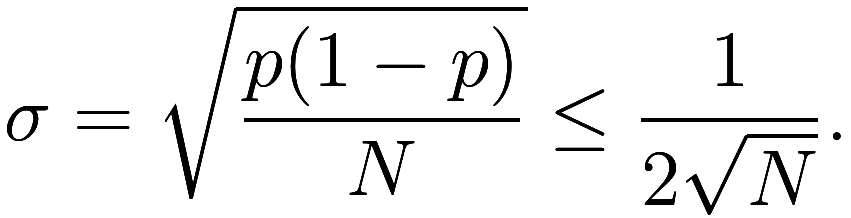
$\sigma = \sqrt{ \frac {p(1 - p)}{N} } \leq \frac 1{2 \sqrt{N}}.$

Note that $\sigma$ is highest when $p = 0.5$ , so we can take that as the worst-case in an upper-bound of $\sigma$ . (The standard deviation describes the typical absolute error $\overline p - p$ : the relative error is highest when $p$ is near 0 or 1. For example if $p = 0.0001$ , it would be easy to over-estimate $p$ by a factor of 10 – but that is a tiny absolute error.) Polls typically report a “margin of error” which is equal to $1.96 \sigma$ and corresponds to the 95% confidence interval. The 1.96 roughly cancels the 2, so one can quickly estimate the margin of error of a poll as the reciprocal of the square root of the poll size: a poll of 1000 people should have about a 3% margin of error.

While we see that the worst-case margin of error depends only on the number of people being polled, many intuitively expect the population size to matter. We give a few such intuitive arguments here, although of course focusing on each one makes its flaws apparent. Then we try to build an intuition for the correct statement, which hopefully yields a better understanding of the difficulties of polling and under what circumstances it can be incorrect.

“It should be more difficult to get information about a larger population, so more poll responses are needed.” It is true that it is more work to get information about a larger population, but rather because each individual response is more work, not because more responses are needed.
“An individual has less chance of being polled, and thus influencing the result, if the poll is of a larger population.” Likewise, an individual has less influence on the larger population’s average opinion.
“All Nebraskans are Americans: so if I need 1000 Nebraskans to learn about Nebraska, and 1000 Americans to learn about the US, why can’t I re-use my Nebraska poll results as a result for the whole US?” Nebraskans are Americans, but they are not randomly sampled Americans. The poll size is fine, but the random selection is not.
“What if I conduct a poll of Americans, and it happens that all my random selections are from Nebraska: surely my results are more informative about Nebraskans than Americans?” It is exceptionally rare for such an event to occur, and the margin of error of a poll only describes its typical error.
“What if I conduct a poll of Americans, and I re-use the results as a ‘poll’ of the poll-respondents: surely my results are more informative about them than about all Americans?” To randomly sample from a population, the population must be a defined group before the sampling process occurs: so “group of people who responded to my poll” is not a population in the sense of statistics.
“How can a poll say something about my opinion if I wasn’t asked?” How indeed? I find this the most compelling incorrect argument. Of course, in a very literal sense this is no objection: the poll results do not claim to say anything about your opinion, but of the average opinion of the whole population. Perhaps we can rephrase this objection as “How can a poll say anything about the average opinion of the group of people who were not asked?”. Our facile response no longer applies, as the-group-of-people-not-polled is so close to the whole population as to have nearly the same average. We could give the same response as in point 5: the-group-of-people-not-polled is not a “population” in the statistical sense. However a better answer, I feel, is that in a certain sense a proper poll does in fact “reach” everyone in the population, whether they know it or not. Hopefully the next section makes this perspective clear.

The common link between the errors with each of these intuitive objections (except point 2) is a misunderstanding of the process of random sampling. We elaborate in the next section.

Random sampling

We are so inundated with poll results that we don’t consider that conducting a poll correctly is very difficult work, as in practice it is impossible to randomly choose someone to poll. Without the ability to truly randomly poll people, pollsters must use poor approximations of randomness to publish any result at all, and thus we have widely varying quality of pollsters according to how many shortcuts they take, what sort of shortcuts these are, and how good pollsters are at adjusting their results to fix the errors these shortcuts introduce.

In practice, the best way to truly randomly select a person from a population would usually be to first make a list of all people in the population, and then choose from this list. However, even the US government in its official decadal census cannot make a list of all people in the US: there were approximately 6.0 million imputations added to the 2010 census, representing people who were not on the census but whose existence was inferred in other ways. In fact, the US uses “randomized” surveys to improve the accuracy of its census, and based on these surveys estimates that 16.0 million people were omitted by the 2010 census: some number of these omissions “may be attributed” to the 6.0 million imputations, but how many is unknown.

This is the key point: a randomly selected person from a group of people must have the potential to have been any member of that group. So to select a random American, the pollster must engage in some process that could, in theory, have resulted in the selection of any American. This is an enormous and insurmountable challenge for a commercial pollster aiming to conduct multiple polls every week, as even the US government’s once-a-decade attempt to make a list of all Americans still fails to reach at least 16 million people.

Thus a poll of the US is much harder than a poll of Nebraska, because the former needs the potential to reach any American, rather than any Nebraskan.

Maybe, if polling a random person within a state isn’t as much work, we can make polling a random American easier by first choosing a random state, and then polling someone in that state. Of course, the states vary in population, so the randomly chosen state should be weighted based on their populations. But how do we know how many people are in each state? Ultimately, knowing the number of people in a state relies (directly or indirectly) on some kind of census or poll or analogous process previously conducted in that state. (This hypothetical illustrates some of the ways pollsters are able to partially re-use previous work to improve accuracy of future polls.)

Polling accuracy

Returning to the original scenario, the chance $p$ that a selected pollee’s opinion is “yes” in the poll does not depend on the number of people who have opinions – that is, the population size. Each additional response has a probability $p$ of being “yes”, and thus gives the same amount of information about the value of $p$ . And regardless of the size of the population, finding the value of $p$ tells the same amount: for a larger population, knowing $p$ tells us less information about each individual in the population.

For the purpose of completeness, we give a brief outline of a proof that the typical error $\sigma_N$ of a poll of size $N$ scales like $\frac 1{\sqrt N}$ . Suppose $\overline {p_1}, \overline{p_2}$ are the averages of two polls each of $N$ people, and $\overline {p} = \frac {\overline{p_1} + \overline{p_2}} 2$ is the average of them taken as aggregate as a single poll of $2N$ people. If $p$ is the true probability of a person responding “yes”, then we have

$4 (\overline p - p)^2 = (\overline p_1 - p)^2 + (\overline p_2 - p)^2 + 2 (\overline p_1 - p) (\overline p_2 - p).$

The term on the left is always positive, with a typical value of about $4 \sigma_{2N}^2$ . Similarly, the first two terms on the right are always positive with typical values of about $\sigma_N^2$ each. As $\overline p_1 - p$ is symmetrically distributed around 0, and the two polls are independent of each other, the last term is equally likely to contribute a positive or negative value to the equation. Thus we have that $4 \sigma_{2N}^2 = 2 \sigma_N^2$ , or $2 \sigma_{2N}^2 = \sigma_N^2$ , so that $\sigma_N$ must scale like $\frac 1{\sqrt N}$ .

(Another way to show that last term does not contribute is to define $\overline p_1' = 2p - \overline p_1$ and $\overline p' = \frac {\overline p_1' + \overline p_2} 2$ ; by symmetry the first is distributed like $\overline p_1$ , and then as the two polls are independent the second is distributed like $\overline p$ . Now repeat the calculation with these definitions: you get the same equation, but the sign of the last term is negative. Adding the two equations gives the desired result. However if one is willing to do all that, one might as well just use the definition of variance and give a formal proof.)

Note on very small populations

What if the population is so small that the “poll” covers the whole population – surely the error is zero then?

In our above discussion, we’ve implicitly assumed that each poll respondent is found independently of the others, so there is a small chance that two of the responses on a poll were given by the same person. Under this assumption, accuracy truly does not depend on population size, and at small populations it simply becomes very likely that some people are polled multiple times. For large populations, the chance of polling the same person becomes tiny.

Real-world polls, whenever feasible, will attempt to make sure that the same people are not polled multiple times, and thus will have slightly higher accuracy at very small populations. This is only relevant when the population size is very close to the poll size, at which point it might be more apt to label the process an incomplete census instead of a random poll.

Follow RSS/Atom feed for updates.