Rotations and balls in even dimensions

2019 December 28

This Christmas, while many of us may be admiring the 3-dimensional balls hung on Christmas trees, let us spare a moment to consider the properties of rotations and balls in even dimensions, and how their properties are simplified by pairing up dimensions. Along the way we will find a surprising identity involving the volumes of even-dimensional balls!

The normal distribution

The first place many students encounter the dichotomy between even and odd dimensions is in statistics class, when studying the normal distribution. Let

$f(x) = \exp(-x^2)$

which is the unnormalized normal distribution: we can think of this as a kind of “fuzzy” one-dimensional ball. To normalize $f(x)$ we need to calculate its “volume”:

$V = \int_{-\infty}^\infty f(x)\ dx.$

The “Gaussian integral” $V$ is a famous problem because the antiderivative of $f$ cannot be expressed in elementary form, but there is a quite clever trick for finding $V$ without using the antiderivative. The idea is to work in two dimensions: as the two-dimensional normal distribution is rotationally symmetric, we can use the symmetry to convert to polar coordinates and solve the problem immediately. We demonstrate this below, where we let $x = r \cos \theta$ and $y = r \sin \theta$ :

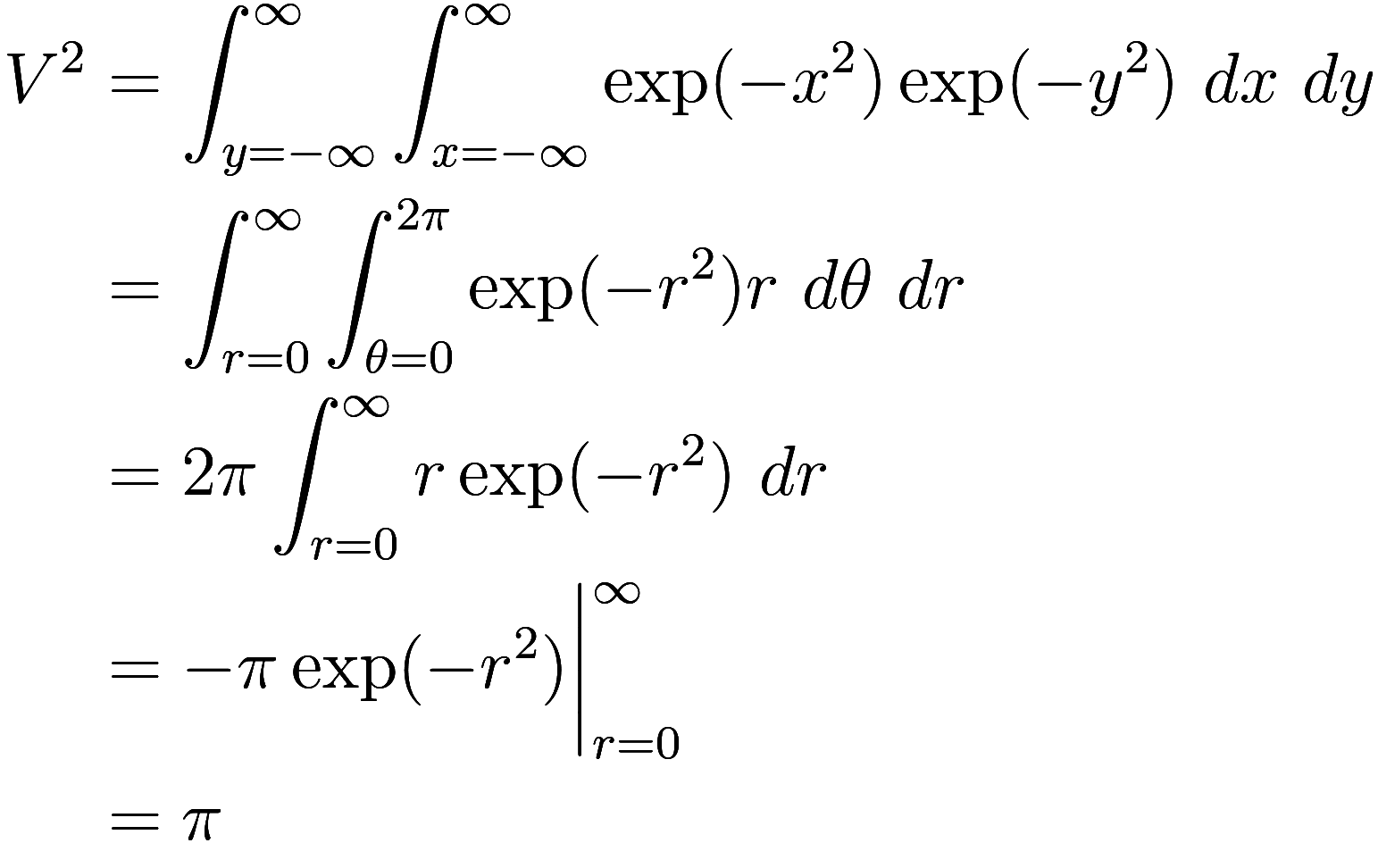
$\begin{aligned} V^2 &= \int_{y = -\infty}^\infty \int_{x = -\infty}^\infty \exp(-x^2) \exp(-y^2)\ dx\ dy \\ &= \int_{r = 0}^\infty \int_{\theta = 0}^{2 \pi} \exp(-r^2) r\ d\theta\ dr \\ &= 2\pi \in...$

Here the factor of $r$ appears because it is the Jacobian of the coordinate transformation from Cartesian coordinates to polar coordinates: a “unit” cell with dimensions $dr$ by $d\theta$ in polar coordinates has an area of $r$ . Formally,

$\begin{vmatrix} \frac{dx}{dr} & \frac{dy}{dr} \\ \frac{dx}{d\theta} & \frac{dy}{d\theta} \end{vmatrix} = \begin{vmatrix} \cos \theta & \sin \theta \\ -r \sin \theta & r \cos \theta \end{vmatrix} = ...$

Thus we find that $V^2 = \pi$ or $V = \sqrt{\pi}$ . This proof is originally due to Poisson, although remarkably it has been proven that the method shown above (of multiplying a definite integral by itself) is totally useless for integrating any other function. This technique is also known in computer science as the Box-Muller transform, where it is commonly used to generate random numbers from a normal distribution: such numbers are generated in pairs, rather than one at a time.

We will see this several more times, where the mathematics can be simplified by taking dimensions in pairs instead of singly. The most obvious example of this – complex numbers – will be discussed near the very end.

Rotations in $n$ dimensions

We have a very strong intuition for rotations in three or fewer dimensions which will not guide us well as we look at higher dimensions.

In one dimension, rotation is not possible: we think of a line as stiff against any possible internal rotation. A creature in one dimension cannot turn around without leaving the line, and is stuck pointing in one direction forever.

In two and three dimensions, a rotation goes around either a point or a line (the “pole”) by a particular angle. If you were to continuously and steadily rotate an object, then after some time (the “rotation period”) it would return to its starting orientation. This is not true above three dimensions!

Fundamentally, the simplest possible rotation takes place in a plane. In three dimensions, you can’t rotate in two different planes at the same time because those planes would intersect in a line, and rotations within a line are impossible. Thus rotations in three dimensions are essentially the same as rotations in two dimensions, except with an extra dimension (the pole) which doesn’t do anything.

In four or more dimensions it is now possible to combine more than one of these planar rotations at the same time. Thus a single rotation could involve one plane rotating by $\alpha$ and another plane rotating by $\beta$ . If you smoothly and steadily rotated a four-dimensional object, and chose rotation rates that were irrational multiples of each other, then the object would never return to its starting orientation.

Again, rotations in five dimensions are much like rotations in four dimensions with an extra dimension which is fixed.

In general, in $2n$ dimensions, for any given rotation $R$ there exists an orthonormal basis $(e_1, \ldots, e_{2n})$ such that $R = R_1(\alpha_1) \cdots R_n(\alpha_n)$ where $R_i(\alpha)$ rotates the plane $\langle e_{2i - 1}, e_{2i} \rangle$ by the angle $\alpha$ . That is, any rotation in $2n$ dimensions is a composition of $n$ rotations, each of which acts on only two dimensions while leaving the others fixed. These rotations $R_i(\alpha)$ all commute with each other.

(In fact, letting the $\alpha$ vary, the group generated by the $R_i(\alpha)$ is isomorphic to $(\mathbb R / \mathbb Z)^n$ , and is a maximal torus of the special orthogonal group $\text{SO}(2n)$ of all rotations in $2n$ dimensions. In particular, it is a maximal commutative subgroup of $\text{SO}(2n)$ : there is no set of $n + 1$ independent rotations in $\text{SO}(2n)$ which commute.)

Another way to express this same concept is that in $2n$ dimensions, any rotation matrix is similar to a block diagonal matrix where the blocks are 2 by 2 matrices of the form:

$\begin{pmatrix} \cos(\alpha) & \sin(\alpha) \\ -\sin(\alpha) & \cos(\alpha) \end{pmatrix}$

This can be proven by noting that the eigenvalues of a rotation all have magnitude 1 (since they are volume-preserving) and come in complex conjugate pairs; so we can diagonalize the matrix in complex numbers and then make pairs of conjugate complex numbers into 2 by 2 blocks of real numbers of the above form.

What happens in $2n + 1$ dimensions? Well, it is exactly the same, except the orthonormal basis has an extra basis element $e_{2n + 1}$ which is fixed by $R$ .

Crystallographic symmetry

A remarkable application of the mathematical theory of rotations arises in the field of crystallography, which curiously stradles the boundary of physics and math. A crystal is a solid object made of a small number of different types of building blocks which are arranged with no “disorder”; that is, their arrangement repeats in a regular way.

(“Disorder” refers to the entropy of the system, and the third law of thermodynamics is often stated that the entropy of a perfect crystal goes to zero as temperature goes to absolute zero. The most common form of ice found on Earth, called icosahedral ice or ice Ih, is actually not a perfect crystal because of the disordered nature of the hydrogen bonds which gives it nonzero entropy at absolute zero. As icosahedral ice is cooled, it can form ice XI, in which the hydrogen bonds are regular.)

The repetitive structure of a crystal is a lattice. Real-world crystal lattices often have some symmetry: for example, table salt has cubic symmetry, which is why chunks of salt tend to come in rectangular shapes. Ice has hexagonal symmetry, causing the six-sided shape of snow flake crystals. However, until 2007, no natural crystal had ever been found with a rotational symmetry other than 2, 3, 4, or 6.

This is a consequence of the crystallographic restriction theorem, which describes precisely in which dimensions it is possible to find a lattice with a specified rotational symmetry. Suppose we want to know in what dimensions there is $m$ -fold rotational symmetry. We factor $m$ into distinct primes as

$m = 2^{a_1} p_2^{a_2} p_3^{a_3} \cdots p_k^{a_k}$

with $a_i > 0$ (except possibly for $a_1$ ); then the minimum dimension $\psi(m)$ with $m$ -fold rotational symmetry is

$\psi(m) = [a_1 > 1] 2^{a_1 - 1} + \sum (p_i^{a_i} - p_i^{a_i - 1}),$

where the first term is $2^{a_1 - 1}$ if $a_1 > 1$ and 0 otherwise (this is Iverson bracket notation). Thus, $\psi(m)$ is defined identically to the Euler totient function $\phi(m)$ except with a sum instead of a product, and a special case for when $m$ is twice an odd number.

(Why a sum instead of product? If you have two rotations with coprime orders that can be performed in $n_1$ and $n_2$ dimensions, then in $n_1 + n_2$ dimensions you can perform the first rotation in the first $n_1$ dimensions and similarly the second rotation in the other $n_2$ dimensions, resulting in a rotation whose order is the product of their orders.)

For example, $\psi(5) = \psi(8) = 4$ show that five-fold rotations and eight-fold rotations first arise in four dimensions, and $\psi(7) = 6$ shows that seven-fold rotations first arise in six dimensions.

In fact, one sees that each of the terms $2^{a_1 - 1}$ and $p_i^{a_i} - p_i^{a_i - 1}$ are even, so their sum $\psi(m)$ is always even. Therefore, lattice symmetries of order $m$ first arise in an even dimension, and an odd-dimensional space doesn’t have any new lattice symmetries that were absent from the previous dimension.

A nascent development in crystallography is the discovery of quasicrystals, which are crystals that violate the crystallographic restriction theorem. These quasicrystals are described by quasilattices, which are not mathematical lattices, but share some of the same properties. Quasilattices are formed by taking an imperfect slice of a higher-dimensional lattice: in this way they acquire forbidden symmetries by taking them from a higher dimension, but the slicing process gives them a sort of regular pattern of imperfections that make them not a true lattice. The most popular example of such a quasilattice is the Penrose tiling:

The Penrose tiling. It has five-fold symmetry, which is forbidden in two dimensions for regular lattices. Image from wikipedia.

The first quasicrystal to be made in the lab was in 1982. The first naturally discovered quasicrystal was in a meteorite in 2007. The only commercial application of quasicrystals so far has been as a non-stick frying pan coating.

A Ho-Mg-Zn quasicrystal. Image from wikipedia.

Volumes of balls

Recall the definition of the unit $n$ -ball,

$B(n) = \{ (x_1, \ldots, x_n) \mid x_1^2 + \cdots + x_n^2 < 1 \}$

and let $V(n)$ be its volume. Certainly the $n$ -ball with radius $r$ has volume $V(n) r^n$ .

We can find $V(n)$ as an integral iterated $n$ times, integrating once over each coordinate, which can be readily solved using induction. Surprisingly (or not?), the induction is easiest when inducting by two dimensions at a time.

Given $V(n)$ , we aim to calculate $V(n + 2)$ . Let $u = x_{n + 1}, v = x_{n + 2}$ be the two new coordinates, and let $r^2 = u^2 + v^2$ and $r^2 + s^2 = 1$ so that $B(n + 2)$ consists of the points where $x_1^2 + \cdots + x_n^2 < s^2$ . Then we have

$\begin{aligned} V(n + 2) &= \int_{r^2 < 1} \left[ \int_{x_1^2 + \cdots + x_n^2 < s^2}\ dx_1 \cdots dx_n \right]\ du\ dv \\ &= \int_{r^2 < 1} V(n) s^n \ du\ dv \\ &= V(n) \int_{r = 0}^1 \int_{\thet...$

where we converted from Cartesian $(u, v)$ coordinates to polar coordinates by $u = r \cos \theta, v = r \sin \theta$ as before. Now if $r^2 + s^2 = 1$ , we have $r\ dr + s\ ds = 0$ , so

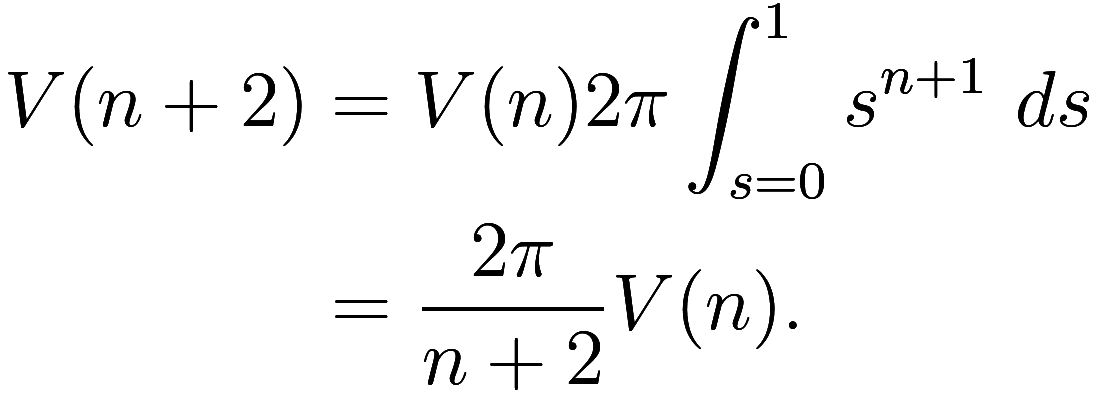
$\begin{aligned} V(n + 2) &= V(n) 2 \pi \int_{s = 0}^1 s^{n + 1}\ ds \\ &= \frac {2 \pi}{n + 2} V(n). \end{aligned}$

Since $V(0) = 1$ , it follows that

$V(2n) = \frac {\pi^n}{n!}.$

Thus the volume of the $n$ -ball decreases faster than exponentially for large $n$ , and so the sum of the volumes of the even-dimensional balls must converge. We find that

$\sum V(2n) = \sum \frac {\pi^n}{n!} = e^\pi,$

and in fact if we use balls with radius $r$ instead of unit balls, the sum of those volumes is $e^{\pi r^2}$ . As a special case, when we use the radius $\frac 1{\sqrt \pi}$ , the sum of the volumes is $e$ !

For completeness sake, we can use $V(1) = 2$ to find

$V(2n + 1) = \frac {2 (n!) (4 \pi)^n}{(2n + 1)!}.$

Why even dimensions? (Gaussian integral and volumes of $n$ -balls)

The common cause for each of these phenomena is the repeated use of 2 in the exponents in several equations, such as the formula for the normal distribution and the Pythagorean formula for finding the distance a point is from the origin.

This becomes apparent by generalizing our definition of distance. In the $\ell_p$ -norm, the distance $|\mathbf x|_p$ of a point $\mathbf x$ from the origin is

$|\mathbf x|_p^p = |x_1|^p + \cdots + |x_n|^p$

with $p = 2$ giving us the ordinary $\ell_2$ -norm. This is defined for $1 \leq p \leq \infty$ ; in the case $p = \infty$ we say that $|\mathbf x|_\infty = \max (|x_1|, \ldots, |x_n|)$ .

When $p$ is an integer, we can evaluate the “Gaussian”-like integral $\exp(-|x|^p)$ by taking the integral to the power of $p$ (the particular case $p = 1$ can be evaluated directly with no special tricks), and the volume of the ball can be inductively calculated by inducting by $p$ dimensions at a time.

We explicitly show how to do the latter calculation. Let

$B_p(n) = \{ (x_1, \ldots, x_n) \mid |x_1|^p + \cdots + |x_n|^p < 1 \},$

the definition of the $n$ -ball in the $\ell_p$ -norm. Let $V_p(n)$ be its volume. As before, we calculate $V_p(n + p)$ from $V_p(n)$ : let $x_1, \ldots, x_n, y_1, \ldots, y_p$ be the coordinates in $n + p$ dimensions, with

$r^p = |y_1|^p + \cdots + |y_p|^p$

and $r^p + s^p = 1$ . Then, as before

$V_p(n + p) = \int_{r = 0}^1 V_p(n) s^n\ dy_1 \cdots dy_p.$

Now the coordinate change is a little messier, because we are no longer using polar coordinates but rather converting to coordinates for the $p$ -ball in the $\ell_p$ -norm. Let $A_p(n)$ be the surface area of the $n$ -ball in the $\ell_p$ -norm, so that

$A_p(n) = \frac d{dr} \left[ V_p(n) r^n \right] = n V_p(n) r^{n - 1}.$

Then we have

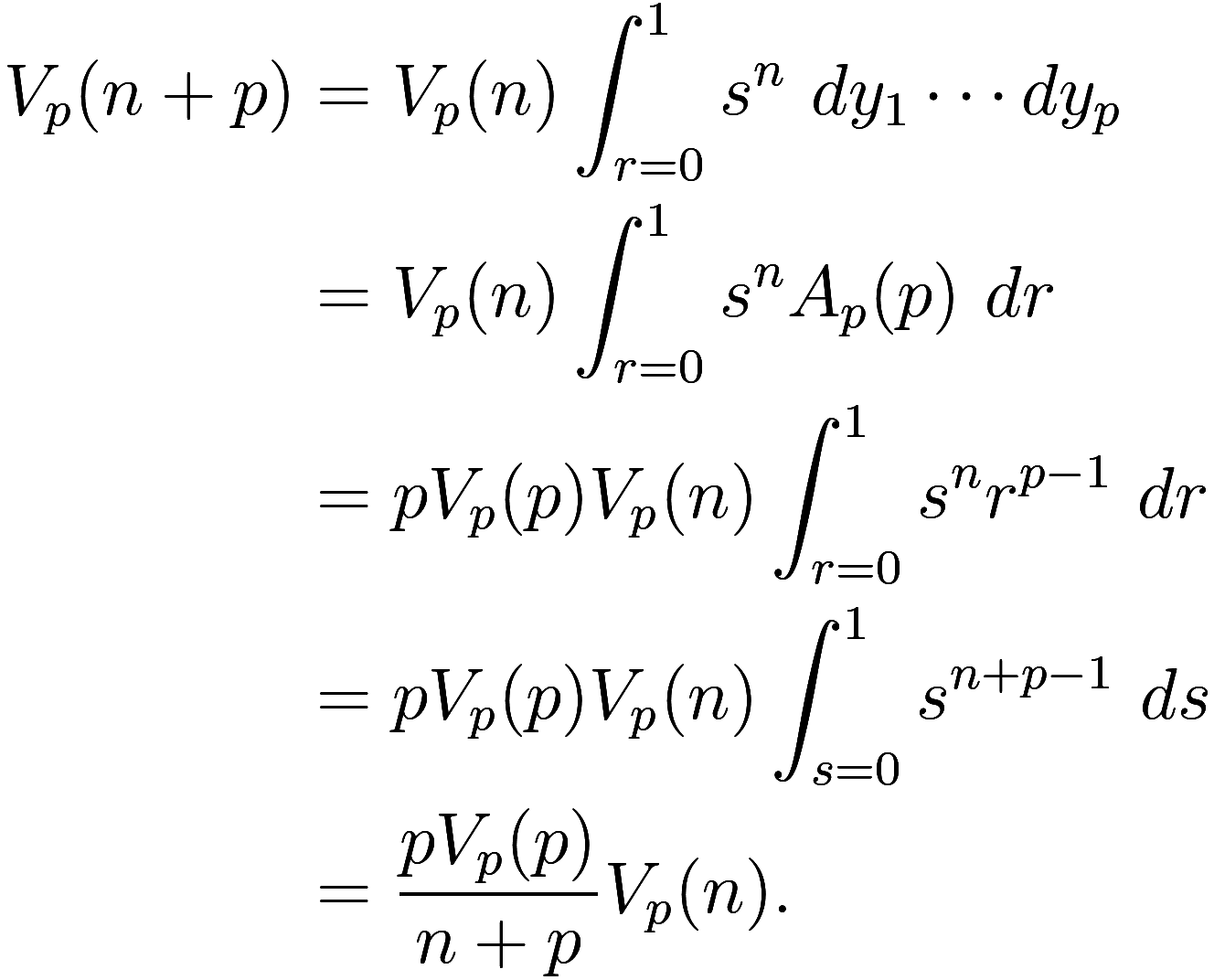
$\begin{aligned} V_p(n + p) &= V_p(n) \int_{r = 0}^1 s^n\ dy_1 \cdots dy_p \\ &= V_p(n) \int_{r = 0}^1 s^n A_p(p)\ dr \\ &= p V_p(p) V_p(n) \int_{r = 0}^1 s^n r^{p - 1}\ dr \\ &= p V_p(p) V_p(n) \i...$

Thus in the same way we have a recurrence from $V_p(n)$ to $V_p(n + p)$ when using the $\ell_p$ -norm. To actually use this, we need the value of $V_p(p)$ . I was unable to easily make progress computing this, but found a paper (Volumes of generalized unit balls) with the result:

$V_p(p) = (2 \Gamma(1 + 1/p))^p.$

(The paper calculates $V_p(n)$ by inducting over $n$ one at a time. The resulting integrals are rather messy compared to the above, but with suitable changes of variable can be made into gamma functions.)

Combining with the inductive relationship, we get

$V_p(np) = \frac 1{n!} (2 \Gamma(1 + 1/p))^{np}.$

Why even dimensions? (Rotations and crystallographic symmetries)

As lattice symmetries, and thus the crystallographic restriction theorem, are consequences of the properties of rotations in $n$ dimensions, this leaves us only with the question of why pairs of numbers are important to rotations.

Rotations are isometries: they preserve distance. (They are also orientation-preserving, that is, don’t make mirror images, but that is not important here). “Distance” here means, as one expects, the ordinary distance in the $\ell_2$ -norm.

Since rotations are defined with respect to the $\ell_2$ -norm, it is natural that the pairing up of dimensions is important to rotations. However, unlike the case with volumes of $n$ -balls, there does not seem to be any sensible way to define rotations with respect to the $\ell_p$ -norm for $p \neq 2$ . Such a space only has trivial isometries (those that permute or negate the coordinates), and it seems that any non-trivial way of creating isometries in $\mathbb R^n$ essentially amounts to partially using an $\ell_2$ -norm and getting some subset of the usual isometries.

Now what makes the $\ell_2$ -norm so special that it is the only way to usefully define rotations? This brings us to the glaring omission in our discussion so far: the complex numbers. Complex numbers are the clearest example in mathematics of when taking a pair of real numbers can greatly simplify a situation that is challenging for single real numbers. While the link between complex numbers and isometries is not readily apparent, as what makes complex numbers unique is their algebraic properties rather than their metric properties, I hope to elucidate what I believe is the key connection.

Consider a linear transformation $T : \mathbb R^n \to \mathbb R^n$ . For $T$ to be an isometry it needs to preserve the length of any element of $\mathbb R^n$ , including in particular its eigenvectors. Thus, its eigenvalues must all have magnitude 1. The eigenvalues of $T$ can be found from its characteristic polynomial:

$P_T(\lambda) = \det (\lambda I - T).$

The roots of $P_T$ are the eigenvalues of $T$ . Finding the roots of a polynomial is an essentially algebraic operation, and for $P_T$ to always have $n$ roots requires moving from $\mathbb R$ to its algebraic closure $\mathbb C$ : working in the real numbers, the most we can guarantee that $P_T$ can be factored is into terms that are quadratic or less. These quadratic terms correspond exactly to the planes within which $T$ rotates.

Each eigenvalue $\lambda \in \mathbb C$ must have magnitude 1 for $T$ to be an isometry. Which norm should we use to calculate the magnitude of $\lambda$ ? For the finite extension $\mathbb C / \mathbb R$ there is only one natural choice of norm, given by taking the product of all of the conjugates of $\lambda$ . If $\lambda = a + bi$ , we have

$N(\lambda) = \lambda \lambda^* = (a + bi) (a - bi) = a^2 + b^2.$

In this way, we see that the $\ell_2$ -norm is inextricably linked to the complex numbers and to isometries in $\mathbb R^n$ .

Even if we try to move from the real numbers to another number system, we run into the Artin-Schreier Theorem: if $F$ is a proper subfield of the complex numbers with finite index, then the index is 2 and $\mathbb C = F[\sqrt{-1}]$ , so exactly the same norm $N(a + bi) = a^2 + b^2$ would be used. Furthermore, any finite extension of a field in its algebraic closure has this same property and is essentially like the real numbers in the complex numbers. Finally, since $\mathbb C$ is algebraically closed, it has no finite extensions, so we can’t build larger finite extensions of the real numbers.

Thus in a fundamental sense all finite dimensional rotations involve repeated copies of the Argand plane representation of the complex numbers, where multiplying by $e^{i \theta}$ rotates by an angle of $\theta$ .

Quaternions

Another remarkable example of simplifying rotations by moving from an odd number of dimensions to an even number is the application of quaternions to simplify the computation of rotations in three dimensions.

As we saw above, any individual rotation in three dimensions can be described as a pole which remains fixed together with an angle in the plane of rotation. If two different rotations have the same pole, they commute with each other and we can compose them by simply adding angles: this is the simple circumstance of rotations in two dimensions. However the general problem of composing rotations in three dimensions requires some thought.

The space $\text{SO}(3)$ of rotations has three dimensions, so we can describe any rotation with three numbers, and there are many ways to do so. The most obvious ways are the axis-angle representation described above, Euler angles which describe a rotation in terms of a succession of rotations around the three coordinate axes, and Tait-Bryan angles which are another way of composing rotations around the three coordinate axes.

Besides the difficulty of computing the composition of two rotations given in the above systems, any chart representing $\text{SO}(3)$ with three numbers cannot cover the whole space of rotations without singularities. These singularities result in gimbal lock, which is a phenomenon in which the coordinate system becomes linearly dependent, and certain degrees of freedom cannot be expressed at the singularities. In addition to being a mathematical problem, this happens to real-world gyroscopes when only three gimbals are used: the positions of the three gimbals is a representation of a rotation with three coordinates, and their exists orientations in which some of the gimbals become redundant, and the gyroscope locks up against rotation in a specific direction. This physical limitation meant that (some of) the Apollo spacecraft would lose orientation information if pointed in specific directions. In fact, when the damaged Apollo 13 was descending to Earth its astronauts were forced to jetison the lunar module (see also: part 1) prematurely because its automatic attitude adjustment was sending the command module too close to gimbal lock, which would have endangered the final descent trajectory.

A gyroscope with three gimbals. Image from wikipedia.

The clever trick to solve this problem is to use four coordinates instead of three. The unit sphere in four dimensions is a double-cover of $\text{SO}(3)$ , so that we can represent a rotation as a vector of four numbers $(a, b, c, d)$ subject to the condition that $a^2 + b^2 + c^2 + d^2 = 1$ ; any particular rotation has exactly two such representations. The surprising feature of this representation is that if we view the vector as a quaternion $a + bi + cj + dk$ , then composition of two rotations is exactly the same as quaternion multiplication.

Quaternions thus give another example of simplifying a problem involving rotations by moving from an odd number of dimensions to an even number. However, any deeper link between the quaternions and the examples given above has eluded me, and for now I can only explain it as a coincidence.

Addendum: reddit user AntiTwister suggested this accessible and informative article which gives the insight to explain why quaternions represent rotations and the appropriate generalization rotors (see geometric algebra) to rotations in any number of dimensions.

Follow RSS/Atom feed for updates.