The greenhouse effect part 4: A model

2022 September 05

Part 1: What is the greenhouse effect? An accessible, scientific introduction
Appendix A: What is the atmosphere?
Appendix B: Ozone
Part 2: Physics of light and temperature
Part 3: Temperature of the Earth without an atmosphere
Part 4: A model of the greenhouse effect
Part 5: Differences between model and reality

In this part we will use what we have learned about light and temperature to create a simple model of the Earth with its atmosphere, which we can solve to see what effect changing the atmosphere has on the temperature of the modeled Earth.

The model is not quantitative, meaning that it is not accurate enough for the numerical results from the model to agree with the true numbers, but it is qualitative, meaning that the overall behavior of the model agrees with the overall behavior of the Earth. Therefore by understanding how the model works we can improve our understanding of the Earth system; in particular, the way the greenhouse effect works in the model is the same way that the greenhouse effect works on the Earth.

Simple model of Earth with atmosphere

Consider the following figure of the Earth¹We mean “the surface of the Earth” when we say “the Earth”, as the interior of the Earth only very slowly exchanges heat with the surface, so it can be ignored. and its atmosphere, with energy flowing between them.

Diagram representing energy flowing between the surface of the Earth, the atmosphere, the Sun, and space.

The arrows in the diagram represent energy flowing between the different objects in the form of light; we ignore other forms of energy transfer²All energy exchanged with the Sun or with space is in the form of light, but some of the energy exchanged between the Earth and the atmosphere is in other forms. In particular, hot water molecules that physically move from the surface into the air bring a large amount of energy with them, called latent heat. Heat conduction plays a lesser role. We also omit geothermal heating, which is energy flowing from the interior of the Earth to the surface. This is estimated to be 47 TW, or 0.092 watts per square meter.. On the left of the diagram is shortwave radiation, that is, visible light. The variable $I$ is the rate at which energy from the Sun is being absorbed by the surface of the Earth; we assume that none of this shortwave radiation is absorbed by the atmosphere. We omit from the diagram light from the Sun that strikes the Earth (or clouds in the atmosphere) and is reflected to space; $I$ is only the portion that is absorbed. Recall from part 3 that

$I = \pi R^2 (1 - \alpha) S.$

On the right of the diagram is longwave radiation, that is, infrared light. The variable $A_\text{up}$ is the rate at which radiation leaves the top of the atmosphere to space; some of this is emitted by the atmosphere, and the rest is emitted by the Earth and passed through the atmosphere. The variable $A_\text{down}$ is the rate at which radiation emitted by the atmosphere strikes the Earth. Finally, the variable $E$ is the rate at which radiation is emitted by the Earth, which will either be absorbed by the atmosphere or transmitted to space.³We briefly remark on the arrows that are absent from the diagram. The most interesting omission is the arrow from the Sun to the atmosphere; we have already commented on that. A tiny fraction of the light emitted to space goes on to strike the Sun or other bodies, but we are uninterested in where exactly it goes once it leaves the Earth. Space is filled with cosmic microwave background radiation, so there should be arrows representing microwave light from space to each of the other objects, but the amount is so tiny as to be totally insignificant – only 1.6 GW of it reaches the Earth, or 3 microwatts per square meter. Finally, the Sun emits a tremendous amount of light into space that does not strike the Earth, but we are not interested in that.

Quantitative estimates of the actual energy flows in and out of the Earth, for context. At left is shortwave radiation, at right is longwave radiation. While we are only be considering radiative transfers, this diagram illustrates that a portion of the Earth-atmosphere energy exchange is non-radiative. It also explicitly includes reflected sunlight, which our diagram had omitted. Diagram by Nasa.

As discussed in part 3 we are interested in the equilibrium of the system, that is, when the total amount of energy entering each object equals the energy leaving that object.

So far we have not made any assumptions about the physics of the atmosphere, so there is insufficient information to solve for the model’s equilibria. However before we go further let us look at what we can conclude so far.

Let $T$ be the average⁴Whenever we say the “average” temperature of a (spherical) object in the context of blackbody radiation, we mean the fourth root of the arithmetic mean of the fourth power of the surface temperature, weighted by surface area and emissivity. That is, we use exactly the average that makes the Stefan-Boltzmann law work with the result. For objects like the Earth, where the temperature does not vary tremendously from one location to another, this average is close to the ordinary arithmetic mean. For tidally-locked or slowly rotating objects like Mercury or the Moon, the distinction can be very important. temperature of the Earth. Then as before, we know that

$E = 4 \pi R^2 \sigma T^4$

where $R$ is the radius of the Earth.

At this point in the calculations in part 3 we solved for the effective temperature $T_e$ that satisfied the equality $E = I$ . However, the introduction of the atmosphere changes this equation. Since the Earth is at equilibrium, the total flow of energy in and out of the surface is equal, giving the equality

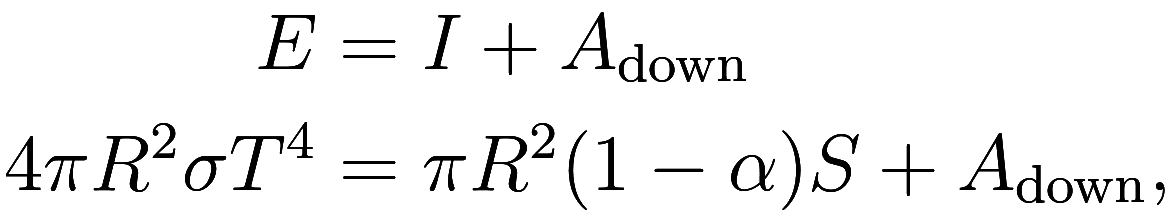
$\begin{aligned} E &= I + A_{\text{down}} \\ 4 \pi R^2 \sigma T^4 &= \pi R^2 (1 - \alpha) S + A_{\text{down}}, \end{aligned}$

where the additional term $A_{\text{down}}$ is downward heating from the atmosphere, which has the effect of increasing the temperature $T$ of the surface of the Earth, demonstrating the greenhouse effect. Our goal is to find the temperature $T$ of the Earth, which will require calculating $A_{\text{down}}$ and $A_{\text{up}}$ .

Since the atmosphere is at equilibrium, we also have

$E = A_{\text{up}} + A_{\text{down}}.$

Combining this equation with $E = I + A_{\text{down}}$ gives us $I = A_{\text{up}}$ , which is to say that the total amount of sunlight the Earth absorbs equals the total amount of light it emits, much as we would expect⁵In fact, direct measurements of light going in and out of the Earth agree with each other up to the accuracy with which they can be measured..

Simple model: no greenhouse gas

To solve for the temperature $T$ of the Earth, we need the values of $A_{\text{down}}$ and $A_{\text{up}}$ , or equivalently we need to know what fraction of the energy $E$ emitted by the Earth is absorbed by the atmosphere or transmitted through it to space. We know that $E = A_{\text{down}} + A_{\text{up}}$ but that is not sufficient information by itself. To find these values we need some kind of additional assumption about the physics of the atmosphere.

The simplest assumption is the total absence of gases that interact with infrared light, so that the atmosphere has no greenhouse gas. In this case, all light from the Earth is transmitted directly to space, and the atmosphere neither absorbs nor emits any infrared light.

In this case, we have $E = A_{\text{up}}$ and $A_{\text{down}} = 0$ . Then $E = I$ and we get exactly the situation of part 3, so that the temperature of the surface of the Earth equals the effective temperature: $T = T_e$ .

Simple model: atmosphere has one layer, with ample greenhouse gas

The next simplest assumption that can be made about the Earth’s atmosphere is to assume that it fully absorbs all upwards emissions from the Earth while maintaining a single uniform temperature, which is usually described by saying it has a “single layer”. Thus $A_{\text{up}}$ consists only of emissions from the atmosphere. As the atmosphere has a uniform temperature, it emits the same amount of energy upwards and downwards, so we get $A_{\text{down}} = A_{\text{up}}$ and

$A_{\text{down}} = \frac 12 E.$

Combining with $E = I + A_{\text{down}}$ we get

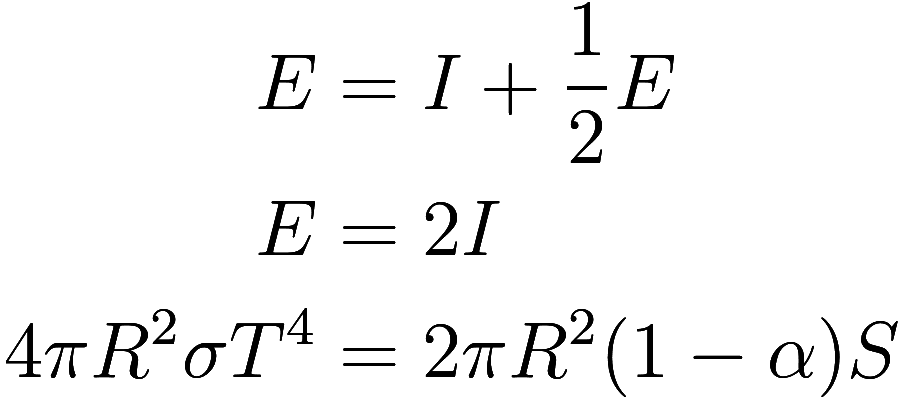
$\begin{aligned} E &= I + \frac 12 E \\ E &= 2I \\ 4 \pi R^2 \sigma T^4 &= 2 \pi R^2 (1 - \alpha) S \end{aligned}$

$T = 2^{1/4} T_e = 1.1892 T_e = 303 \text{ K}.$

This is 30 C or 86 F, somewhat above the true average temperature of the Earth.

Simple model: atmosphere has one layer, with only some greenhouse gas

Let us assume again the the atmosphere is a single layer of uniform temperature, but now suppose it does not have sufficient greenhouse gas to fully absorb all infrared emissions from the Earth. Let $\lambda$ be the fraction of such emissions that are absorbed, so that the atmosphere absorbs $\lambda E$ and transmits $(1 - \lambda)E$ . Since half of the atmosphere’s emissions are downwards (by the uniform temperature assumption again), we get $A_{\text{down}} = \frac \lambda 2 E$ , so that

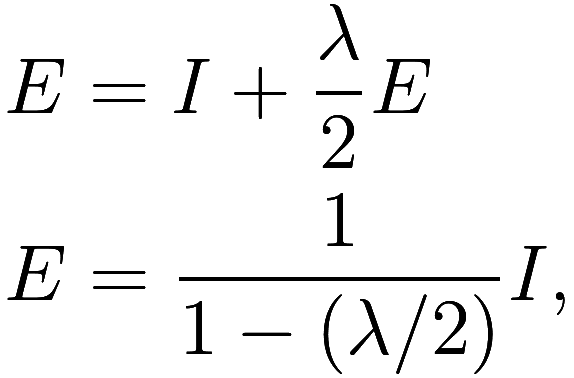
$\begin{aligned} E &= I + \frac \lambda 2 E \\ E &= \frac 1 {1 - (\lambda / 2)} I, \end{aligned}$

and therefore $T = (1 - (\lambda / 2))^{-1/4} T_e$ .

When $\lambda = 0$ , we recover the situation of the model with no greenhouse gas, and get $T = T_e$ . When $\lambda = 1$ , we find again the result of the model with ample greenhouse gas, and get $T = 2^{1/4} T_e$ . As we vary the amount of greenhouse gas in the atmosphere from none to ample, $\lambda$ varies between 0 and 1, and the temperature calculated from the model varies from $T_e$ to $2^{1/4} T_e$ , increasing as greenhouse gas is added. This illustrates how adding greenhouse gases to the atmosphere causes the temperature to rise.

Multiple layers

With the single-layer assumption we saw that the Earth’s temperature increased with additional greenhouse gases up to a fixed maximum. However, as more and more greenhouse gas is added to the atmosphere, the assumption that the atmosphere can maintain a uniform temperature would break down as the emissions from the Earth can’t penetrate past the very bottom of the atmosphere.

If we instead approximate the atmosphere as being composed of multiple layers, each fully absorbing all incident infrared radiation and individually have uniform temperatures, then each such successive layer of greenhouse gases causes the temperature to increase by a factor of $2^{1/4}$ . Equivalently, every fourth layer doubles the temperature.

Similarly, we could modify the model to accommodate anti-greenhouse gases⁶Hazy conditions can have an anti-greenhouse-like effect, although the mechanism is not exactly the same; for example, major volcanic eruptions cool the Earth for a few years by putting sulfur aerosols in the stratosphere. which absorb shortwave radiation and transmit longwave radiation. Each such layer of anti-greenhouse gases decreases the temperature by a factor of $2^{-1/4}$ , countering the effects of one layer of greenhouse gases.

We mean “the surface of the Earth” when we say “the Earth”, as the interior of the Earth only very slowly exchanges heat with the surface, so it can be ignored.↩︎
All energy exchanged with the Sun or with space is in the form of light, but some of the energy exchanged between the Earth and the atmosphere is in other forms. In particular, hot water molecules that physically move from the surface into the air bring a large amount of energy with them, called latent heat. Heat conduction plays a lesser role. We also omit geothermal heating, which is energy flowing from the interior of the Earth to the surface. This is estimated to be 47 TW, or 0.092 watts per square meter.↩︎
We briefly remark on the arrows that are absent from the diagram. The most interesting omission is the arrow from the Sun to the atmosphere; we have already commented on that. A tiny fraction of the light emitted to space goes on to strike the Sun or other bodies, but we are uninterested in where exactly it goes once it leaves the Earth. Space is filled with cosmic microwave background radiation, so there should be arrows representing microwave light from space to each of the other objects, but the amount is so tiny as to be totally insignificant – only 1.6 GW of it reaches the Earth, or 3 microwatts per square meter. Finally, the Sun emits a tremendous amount of light into space that does not strike the Earth, but we are not interested in that.↩︎
Whenever we say the “average” temperature of a (spherical) object in the context of blackbody radiation, we mean the fourth root of the arithmetic mean of the fourth power of the surface temperature, weighted by surface area and emissivity. That is, we use exactly the average that makes the Stefan-Boltzmann law work with the result. For objects like the Earth, where the temperature does not vary tremendously from one location to another, this average is close to the ordinary arithmetic mean. For tidally-locked or slowly rotating objects like Mercury or the Moon, the distinction can be very important.↩︎
In fact, direct measurements of light going in and out of the Earth agree with each other up to the accuracy with which they can be measured.↩︎
Hazy conditions can have an anti-greenhouse-like effect, although the mechanism is not exactly the same; for example, major volcanic eruptions cool the Earth for a few years by putting sulfur aerosols in the stratosphere.↩︎

Follow RSS/Atom feed for updates.