The greenhouse effect part 3: Temperature of the Earth without an atmosphere

2022 August 29

Part 1: What is the greenhouse effect? An accessible, scientific introduction
Appendix A: What is the atmosphere?
Appendix B: Ozone
Part 2: Physics of light and temperature
Part 3: Temperature of the Earth without an atmosphere
Part 4: A model of the greenhouse effect
Part 5: Differences between model and reality

Equilibrium temperature

So far we have been using temperatures without any discussion about what temperature is or what it measures. Though the technical details of temperature are tricky, in everyday life and for our purposes we can consider temperature as a measure of how much thermal energy is in an object. There are two important properties of temperature: adding heat to an object causes its temperature to increase¹One major exception is phase changes like ice melting or liquid water evaporating; another of course is black holes, as mentioned earlier., and when two objects are allowed to freely exchange energy then heat will flow from the hotter object to the colder object. As we discussed in part 2, if these two properties were not true then life would not be possible.

We say an object is in thermal equilibrium with its surroundings if its temperature is not changing over time. This is the same thing as saying there is no net flow of heat in or out of the object. What happens if an object was at thermal equilibrium but is transiently heated up? The object is hotter than before and will therefore lose heat faster than before; for example, through blackbody radiation, which is greater the hotter an object is. Since the object will now have a net flow of heat outwards, it will cool down over time. Similarly, if an object was at thermal equilibrium and is transiently cooled down, it will experience a net flow of heat inwards and heat up over time.

Therefore we expect that in general an object will have a unique equilibrium temperature, that is, the one temperature at which it would be at thermal equilibrium with its surroundings. Above this temperature, the object will cool down, and below this temperature, the object will heat up, and at this temperature the object will be in thermal equilibrium. The equilibrium temperature depends on the object’s surroundings and the interactions between the object and its surroundings. If these change, then the equilibrium temperature can also change. For example, consider a room heated by a heater on a cold day; the room reaches some steady temperature at which the heat it gains from the heater is balanced by the heat lost to the outside. Opening a window decreases the equilibrium temperature, so the room will cool off until it approaches this new equilibrium temperature.

By analyzing the equilibria of a system we often find it much easier to understand how the system changes over time. The most direct approach to studying the changes in a system, which I would call the “dynamic” method, is to determine the current state of the system and how that state is changing. For example, if we know the current temperature of an object, and we know how the temperature is changing, then we can predict the future temperature of the object. Alternatively we can analyze the equilibria of a system, which I call the “static” method. The static method loses information about transient fluctuations or detailed behavior of the system, but it often is better at giving an overall understanding of the behavior of the system. The static method is also usually easier and more robust to model error²Model error refers to details of the real-world system which are omitted in the mathematical model. Regardless of how detailed and precise the model is, for a model to be useful there will always be some further detail that is missing..

In the specific example of studying the temperature of the Earth, the dynamic method requires knowing the current temperature of the Earth, exactly how much energy the Earth is receiving from the Sun at each point in time, and exactly how much energy the Earth is losing to space at each point of time. Knowing these three things we can calculate the temperature of the Earth at any point in the future. Of course, this is totally infeasible because, for example, the amount of sunlight reflected back into space depends on how many clouds there are and what shape they have, which rapidly changes within hours. If we tried to make predictions in this way they would become wildly inaccurate almost immediately because any small error compounds upon itself (Which is not to suggest that such predictions are impossible, just that this naive approach is not viable.).

Alternatively, using the static method we first measure how much energy the Earth is typically receiving from the Sun, and then calculate the temperature at which the Earth would emit as much energy as it is receiving. This calculation tells us the equilibrium temperature of the Earth, that is, the temperature at which it radiates the same amount of energy as it receives, so that the Earth’s temperature does not change. While this method does not explain any oscillations or fluctuations around the predicted equilibrium temperature, it does capture the most important features that are relevant to the Earth’s temperature.

Temperature of the Earth with no atmosphere

We now have the pieces to understand what temperature the Earth would have in the absence of an atmosphere. The Earth gains energy through light received from the Sun; some of this light is reflected back to space but most of it is absorbed by the Earth’s surface. The proportion of light reflected back to space is called the albedo of Earth, and it equals approximately 30%³Of course, if the Earth had no atmosphere it would have a significantly different albedo, among many other major differences.. The Earth loses energy by radiating it to space due to the blackbody effect, that any warm object emits light; the amount of energy lost this way depends on the Earth’s temperature. The equilibrium temperature of the Earth is the temperature at which the energy gains from the Sun are equal to the energy losses due to the blackbody effect.

The rate at which energy is received from the Sun is equal to

$\pi R^2 (1 - \alpha) S$

where $R$ is the radius of the Earth, $\alpha$ is the albedo of the Earth, and $S$ is the insolation of the Earth (the amount of energy in sunlight received by the Earth, per area and per time). The reason for the factor of $\pi R^2$ is that, from the perspective of the Sun, the Earth appears to be a disc of radius $R$ , so that $\pi R^2$ is the total effective area illuminated by the Sun⁴While the surface area of the Earth is $4 \pi R^2$ and half of that is exposed to sunlight at any time, the amount of sunlight a location receives depends on the angle the Sun is above the horizon, and the average illuminated location receives half as much light as it would receive under direct, full sunlight.. Since the albedo $\alpha$ is the proportion of light reflected back to space, $1 - \alpha$ is the proportion absorbed.

From the Stefan-Boltzmann law, the rate at which energy is radiated from the Earth due to the blackbody effect is

$4 \pi R^2 \sigma T^4$

where again $R$ is the radius of the Earth, $\sigma$ is the Stefan-Boltzmann constant, and $T$ is the temperature of the Earth. Here $4 \pi R^2$ is the surface area of a sphere with radius $R$ .

At the equilibrium temperature $T_e$ the energy received and emitted is equal, so

$\pi R^2 (1 - \alpha) S = 4 \pi R^2 \sigma T_e^4.$

If we know the values of $\alpha, S,$ and $\sigma$ we can solve for $T_e$ :

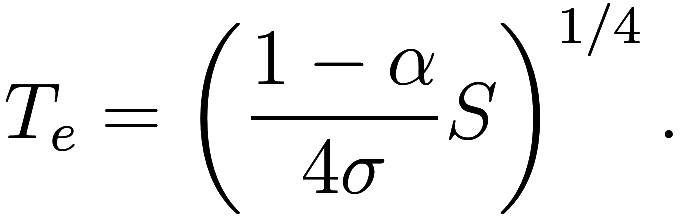
$T_e = \left(\frac {1 - \alpha}{4 \sigma} S\right)^{1/4}.$

Observe that the radius $R$ of the Earth has no effect; if the Earth were larger, it would absorb more sunlight and also emit more blackbody radiation.

If we use sensible values⁵We take albedo $\alpha = 0.3$ , insolation $S = 1366 \text{ W m}^{-2}$ , and Stefan-Boltzmann constant $\sigma = 5.67 \cdot 10^{-8} \text{ W m}^{-2} \text{K}^{-4}$ . As per a previous note, we use an emissivity $\epsilon = 1$ . With a more realistic $\epsilon = 0.96$ , we get $T_e = 257$ K. for $\alpha, S,$ and $\sigma$ , we compute the equilibrium temperature

$T_e = 255 \text{ K}$

or -18 C or -1 F.

The temperature of an astronomical body computed in this way, by ignoring all atmospheric effects, is called the effective temperature; specifically, we find the effective temperature of an object by measuring how much light it emits and using the Stefan-Boltzmann law to determine the temperature needed to emit that much light. In fact, when we previously spoke about the temperature of the surface of the Sun, we really meant the effective temperature of the Sun⁶Like the gas planets, the Sun does not have a solid surface, but instead gradually becomes denser and more opaque closer to the center. The “surface” is defined somewhat arbitrarily in terms of a certain level of opacity. The exact temperature at this depth would be difficult to measure, but is likely very close to the effective temperature.. A distant astronomer attempting to measure the temperature of the Earth would be measuring its effective temperature.

The effective temperature of the Earth differs from the true temperature of the surface of the Earth in two important ways:

The effective temperature is a single number, while the true temperature varies with location.
The surface temperature is affected by the atmosphere, in particular the greenhouse effect.

The effective temperature can be thought of as a suitable average⁷Rather than the typical arithmetic mean, the fourth root of the arithmetic mean of the fourth powers is the suitable average. This is always warmer than the arithmetic mean, although not significantly so for the Earth. of the temperature across all locations. These spatial variations are important to weather and the climate but do not directly pertain to the greenhouse effect, so we will not discuss them here.

One major exception is phase changes like ice melting or liquid water evaporating; another of course is black holes, as mentioned earlier.↩︎
Model error refers to details of the real-world system which are omitted in the mathematical model. Regardless of how detailed and precise the model is, for a model to be useful there will always be some further detail that is missing.↩︎
Of course, if the Earth had no atmosphere it would have a significantly different albedo, among many other major differences.↩︎
While the surface area of the Earth is $4 \pi R^2$ and half of that is exposed to sunlight at any time, the amount of sunlight a location receives depends on the angle the Sun is above the horizon, and the average illuminated location receives half as much light as it would receive under direct, full sunlight.↩︎
We take albedo $\alpha = 0.3$ , insolation $S = 1366 \text{ W m}^{-2}$ , and Stefan-Boltzmann constant $\sigma = 5.67 \cdot 10^{-8} \text{ W m}^{-2} \text{K}^{-4}$ . As per a previous note, we use an emissivity $\epsilon = 1$ . With a more realistic $\epsilon = 0.96$ , we get $T_e = 257$ K.↩︎
Like the gas planets, the Sun does not have a solid surface, but instead gradually becomes denser and more opaque closer to the center. The “surface” is defined somewhat arbitrarily in terms of a certain level of opacity. The exact temperature at this depth would be difficult to measure, but is likely very close to the effective temperature.↩︎
Rather than the typical arithmetic mean, the fourth root of the arithmetic mean of the fourth powers is the suitable average. This is always warmer than the arithmetic mean, although not significantly so for the Earth.↩︎

Follow RSS/Atom feed for updates.