Percolation theory and fractal dimension

2024 February 29

(As mentioned before, current MIT students should not read this material.)

Exercises on random walks
Percolation theory and finding the critical point
Percolation theory and fractal dimension
The coastline paradox
Ant in a labyrinth: random walk with invasion percolation

Having looked at how the largest cluster size $C_1$ varies with $p$ for a fixed $L$ , now we consider the converse of what happens as $L$ varies for a fixed $p$ .

We learned in class that $C_1$ follows certain functional forms in the limit of large $L$ :

$\begin{aligned} C_1(L) &\sim \log L &&p < p_c \\ C_1(L) &\sim L^D &&p = p_c \\ C_1(L) &\sim L^d &&p > p_c \end{aligned}$

Here, $d$ is the dimension of the grid being used, and $D < d$ is the fractal dimension of the critical percolating cluster¹The fractal scaling $L^D$ is just one of many power laws that describe the behavior of a percolating cluster at or near the critical point. The exponents of these power laws are referred to as “universal” critical exponents because their value does not depend on the local shape of the grid being used as a substrate, but only on the grid’s dimension; thus all two-dimensional grids follow the same power laws. For $d \geq 6$ , the exponents stop depending on the dimension, and equal the values according to mean-field theory. Generally speaking we only have exact results for $d = 2$ , where conformal field theory can be used, or $d \geq 6$ where mean-field theory is correct..

As an aside, it is worth noting that this behavior for $C_1$ is not obvious, and it is plausible for there to exist a range of values of $p$ which exhibit large clusters²i.e., cluster sizes distributed like a power law, and therefore $C_1$ would be a power law in $L$ without having infinite clusters. It wasn’t until the 1980s that is was proved³eg “Sharpness of the Phase Transition in Percolation Models” by Michael Aizenman and David J. Barsky that there was a single phase transition at a single critical point $p_c$ at which clusters go immediately from being small to infinite.

Can we observe these functional forms empirically? Let us start in 2D, and graph how $C_1$ and $C_2$ (the second-largest cluster size) vary with $L$ for $p = 0.4$ .

We have shown the least-squares fit of $C_1$ as a linear function of $\log L$ for large $L$ ; it is quite a good fit. $C_2$ also appears to grow like $\log L$ , although I did not perform a fit.

Moving up to $p = 0.56$ :

We are now fitting $C_1$ against two different functional forms. Where $C_1$ is almost as large as one would expect at the critical point, we are fitting $C_1$ against a power law; where $C_1$ is significantly smaller than one expects at the critical point, we fit against $\log L$ ⁴Specifically, we use a power law where $q_1$ is at least 80% of $q_1$ at $p_c$ for that $L$ , and $\log L$ where $q_1$ is at most 20% of $q_1$ at $p_c$ for that $L$ .. Again, for large $L$ we see that $C_1$ is a good fit against $\log L$ .

At $p = 0.58$ :

It is hard to say at this point that $C_1$ is a good fit for $\log L$ ; at this point it is looking more and more like a power law.

Finally we get to $p = 0.59$ :

An excellent fit to a power law! Or at least, it looks like an excellent fit until it is compared to the fit with $p = 0.5927$ , very close to $p_c = 0.592746$ :

Note that this graph extends to a much higher value of L than the other graphs. — Note that this graph extends to a much higher value of $L$ than the other graphs.

I find it remarkable how much of a difference there is between 0.59 and 0.5927; the former has a very slight but visible bend to the graph as $C_1$ starts to fall behind slightly for large $L$ . Also, one can see that $C_2$ and $C_1$ are not quite parallel when $p = 0.59$ ; $C_2$ is slowly but surely catching up on $C_1$ . But at $p = 0.5927$ however, $C_1$ and $C_2$ both perfectly match a power law for as high a value of $L$ as my computer could handle, and visually appear exactly parallel⁵Though from the exponent we see $C_2$ is in fact slightly catching up on $C_1$ . This is because at $p = p_c$ the system exhibits scale invariance.

What of the fractal dimension? We estimate $D = 1.89406$ , just shy of the correct value known to be exactly $D = 91 / 48 = 1.8958333$ .

Continuing, as soon as $p = 0.60$ it is already obvious we have overshot $p_c$ :

And it just gets more obvious as $p$ increases; at $p = 0.61$ the second-largest cluster can no longer keep up:

Here we see that $C_1 \sim L^{1.98}$ , very close to the predicted relation of $C_1 \sim L^2$ for $p > p_c$ .

Of course, the same observations hold in 3D. Here is the behavior at the critical point:

Now we can use these graphs to resolve a bit of a mystery. We saw previously that for any fixed $L$ , $q_1$ varies continuously as a function of $p$ . However, the theoretical functional forms for $C_1$ do not vary continuously: they abruptly change from $\log L$ when $p < p_c$ to a power law at $p = p_c$ . How can we resolve this disparity?

It appears from these graphs that we were wrong about the functional forms, and the functional form actually does change continuously; first $C_1$ fits $\log L$ well for small $p$ , then gradually becomes more like a power law as $p$ approaches $p_c$ . However this isn’t true – the functional forms as stated above are correct. What actually happens is that although the functional form for large $L$ does abruptly change at $p = p_c$ , as $p$ gets closer to $p_c$ then how large $L$ needs to be for the functional form to be applicable grows considerably.

This is related to the notion of uniform convergence; while $q_1$ is a continuous function of $p$ for any fixed $L$ , as we take the limit $L \to \infty$ , $q_1$ converges to a discontinuous function. This is because the convergence is not uniform,⁶necessarily, as uniform convergence of continuous functions always gives a continuous function but rather the convergence is slower for $p$ near $p_c$ .

How large $L$ needs to be to be considered “large” is called the correlation length $\xi$ ; we find it by asking the question, what is the probability that two occupied sites belong to the same cluster⁷More rigorously, how much more likely are they to be in the same cluster than two far-away points are in the same cluster? This is the same question when $p < p_c$ , but for $p \geq p_c$ two distant points have a nonzero chance of lying in the same cluster because there is an infinite cluster. Thus what we are really asking is the chance two sites lie in the same finite cluster.? If they are further than $\xi$ apart, the probability falls exponentially with the distance between them, like $e^{-r / \xi}$ . Another way to see this is that the radius of a random cluster tends to be at most around $\xi$ ⁸or a suitable power thereof.

Therefore when $\xi$ is as big as $L$ , the largest finite clusters tend to span the whole grid, and the system behaves roughly as if it were at $p = p_c$ . Only for $L \gg \xi$ can we observe the limiting behavior.

$\xi$ itself obeys a power-law relationship (see the above footnote on universal critical percolation exponents):

$\xi \sim \left| p - p_c \right|^{-\nu}$

where $\nu = 4 / 3$ for all 2D grids. Thus when $p = 0.59$ we find $\xi \approx 2600$ and would need $L$ to be significantly larger than that to observe the $\log L$ behavior, whereas our graph only extended to $L = 1000$ .

We can see this with a 3D plot of $C_1$ :

The ramp region with $p > p_c$ corresponds to a power law growth rate, and the constant slope of 2 shows that that whole region has the same exponent of $d = 2$ . The flatter region with $p < p_c$ has an asymptotic growth rate of $\log L$ . As $L$ gets larger, the transition between the flat region and the ramp becomes sharper and sharper, but for any fixed value of $L$ it remains continuous and unbroken.

Why log L?

The $L^d$ behavior for $p > p_c$ is clear, as each occupied site has some fixed, high probability $q_1$ of being in the big cluster, so $C_1 = q_1pL^d$ scales with the volume of the domain $L^d$ . To understand the transition from $\log L$ to $L^d$ better let us see if we can explain the $\log L$ behavior.

The key observation is that when $p < p_c$ , far away sites are unlikely to belong to the same cluster; the probability decays exponentially with distance between the sites, so as $L \to \infty$ most sites become uncorrelated. Thus we can imagine each of the clusters as being (mostly) independent of each other. There is some finite average size for a cluster, so as $L$ is increased the number of clusters $n$ grows proportionally to the volume of the domain:

$n \sim L^d.$

So to find the largest cluster, imagine taking $n$ iid samples $X_1, \ldots, X_n$ from some probability distribution $f(x)$ of cluster sizes. $f(x)$ will be somewhat “nice” in that it has finite mean, finite variance, and goes to 0 rapidly as $x \to \infty$ .

Let $M_n$ be the maximum of the $X_i$ ; we wish to find the probability distribution $g(x)$ of $M_n$ . Now certainly by definition of $M_n$ ,

$P(M_n < x) = P(\text{each } X_i < x) = P(X_1 < x) \cdots P(X_n < x) = P(X_1 < x)^n$

where we have used independence of the $X_i$ and identity of the $X_i$ . Note that $P(x_1 < x)$ is simply the cumulative distribution function of $f$ , i.e., its integral.

Let $x_0$ be the median of $M_n$ . Then

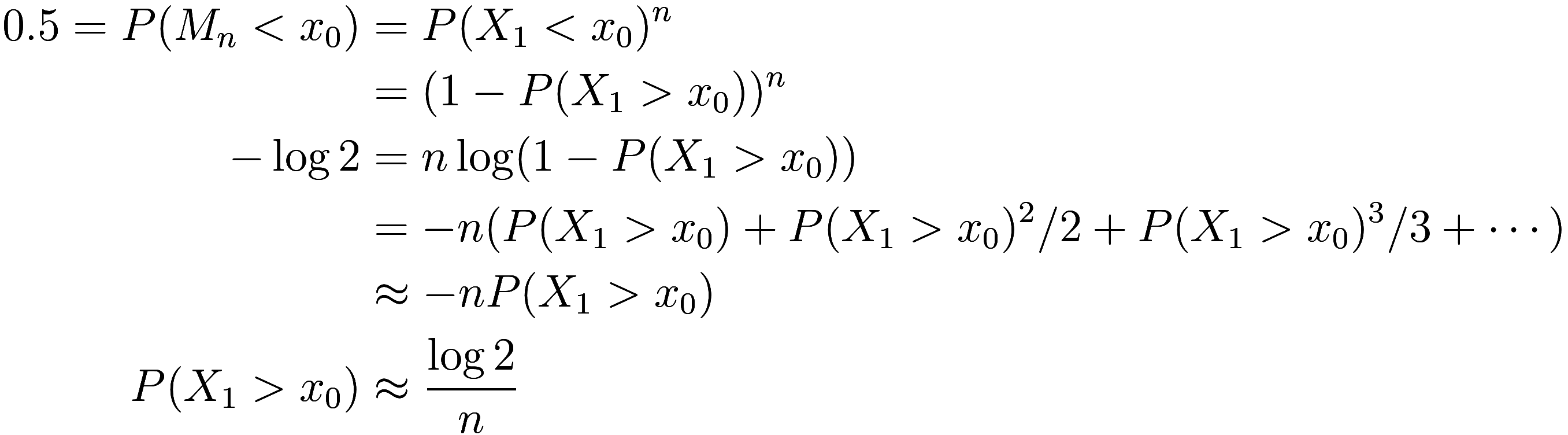
$\begin{aligned} 0.5 = P(M_n < x_0) &= P(X_1 < x_0)^n \\ &= (1 - P(X_1 > x_0))^n \\ - \log 2 &= n \log (1 - P(X_1 > x_0)) \\ &= -n (P(X_1 > x_0) + P(X_1 > x_0)^2 / 2 + P(X_1 > x_0)^...$

We have used the Taylor series for $\log$ ; the approximation is accurate because $n$ is extremely large and so $P(X_1 > x_0)$ is extremely small.

So now we need to know the asymptotic behavior of $f(x)$ . A logical guess is that $f$ is a normal distribution. In that case, its cdf is called the error function (after scaling and translating appropriately), in this context more specifically called the Q-function. An excellent approximation for the tail behavior of $Q$ is $Q(x) \approx \phi(x) / x$ where $\phi(x)$ is the standard normal distribution, so we get

$\begin{aligned} \frac {\log 2}{n} \approx P(X_1 > x_0) &\stackrel{?}{=} Q\left(\frac {x_0 - \mu}{\sigma}\right) \\ &\approx \phi\left(\frac{x_0 - \mu}{\sigma}\right) \frac {\sigma}{x_0 - \...$

Recall $x_0$ is the median of the maximum cluster size, and that $n \sim L^d$ . In the end we find that $C_1 \sim \sqrt{\log L}$ … which is not correct!

So our guess that cluster sizes are normally distributed is not good; the normal distribution has too little weight in the tails.

Let us see if we can derive the tail behavior of $X_1$ from first principles. To start, suppose we are in 1D, and we have $p < p_c = 1$ .

Consider an occupied site, and for simplicity ignore its left neighbor. For it to be part of a cluster of size $k$ , the $k - 1$ sites to the right must all be occupied, which has probability $p^{k - 1}$ . Each step further imposes another factor of $p$ , so $f$ is an exponential distribution. That is, $f(x) \sim e^{-x}$ , and likewise its integral $P(X > x) = cdf_f(x) \sim e^{-x}$ . This gives:

$\begin{aligned} \frac {\log 2}{n} &\sim e^{-x_0} \\ x_0 &\sim \log n \sim \log L \end{aligned}$

which is now correct.

What about higher than 1D? The whole difficulty with $d > 1$ is the presence of loops in the grid, i.e., there is more than one route between any two particular sites. If there were only one route connecting two sites it would be very easy to predict whether they are in the same cluster.

Thus we turn to the Bethe lattice, which is the infinite tree where each vertex has $z$ neighbors. If we take $z = 2d$ , then the Bethe lattice strongly resembles the $d$ -dimensional grid, in that both are regular graphs with vertex degree $2d$ . In fact, the Bethe lattice is the universal covering graph of the integer lattice; that is, it was what you get when removing all the loops from the integer lattice. E.g., if you go up, right, down, left on the Bethe lattice you do not return where you started – the only way to return to the origin is to exactly retrace your steps.

The Bethe lattice being a tree, there is a unique path connecting any two sites, which again makes it easy to calculate the cluster size distribution. An occupied site has $z$ neighbors, each with a probability $p$ of being occupied. Each “newly” occupied neighbor opens up an additional $z - 1$ new neighbors which have the potential to be occupied themselves. We can model this process of growing a cluster as a weighted random walk that starts $z$ units to the right of the origin and at each time step has a $p$ probability of going $z - 2$ units to the right and $1 - p$ probability going 1 unit to the left; the size of the cluster is one plus the number of times the random walk went to the right before reaching the origin.⁹The distance from the origin represents the number of sites adjacent to the incomplete cluster that have not yet been determined whether they are occupied or not. Thus the size of the cluster is $1 + (t - z) / (z - 1)$ where $t$ is the time it takes for the random walk to reach the origin.

For $p < 1 / (z - 1)$ , which is the critical threshold for the Bethe lattice, this random walk is biased towards the left. The path of a biased random walk can be thought of as diffusing from a mean position which is moving with time. For large times $t$ , this mean position is $O(t)$ to the left of the origin (specifically, the mean position is at $z - t (p(z - 1) - 1)$ ), but the standard deviation only grows like $O(\sqrt t)$ , like all random walks / diffusion processes. Therefore to remain to the right of the origin at time $t$ requires being $O(\sqrt t)$ standard deviations to the right. Since diffusion creates a normal distribution, the probability of remaining $\sqrt t$ standard deviations from the mean scales like

$e^{-(\sqrt t)^2 / 2} = e^{-t / 2}$

which is an exponential decay, exactly as we saw in 1D (recall that the time it takes this random walk to cross the origin is proportional to the size of the cluster).

Thus we have recovered the desired $\log L$ scaling for clusters in the Bethe lattice, but how does this help us with the standard integer lattice when $d > 1$ ?

Let $\alpha$ be the universal cover that maps the Bethe lattice to the integer lattice (i.e. $\alpha$ “curls up” the Bethe lattice by restoring all the loops), and consider a random cluster $C_B$ on the Bethe lattice. Let $\alpha(C_B)$ be the cluster on the integer lattice consisting of the points $\alpha(v)$ for $v$ in $C_B$ .¹⁰Note that if some collection $C_B$ of points in the Bethe lattice are connected, then $\alpha(C_B)$ is also connected, because $\alpha$ is a covering map and therefore sends paths to paths. Certainly $\alpha(C_B)$ is either the same size or smaller than $C_B$ , depending on whether different points in $C_B$ have the same image. (Eg, recall that the paths “right, right, up, up” and “up, up, right, right” go to different points on the Bethe lattice, and the same point on the integer lattice.)

Now $\alpha(C_B)$ is some sort of a random cluster, but is it drawn from the same probability distribution as randomly generated clusters on the integer lattice? No, in fact it tends to be larger. Specifically, if we fix an origin point $v_0$ ¹¹As a slight abuse of notation we will use $v_0$ to mean the origin of both the Bethe lattice and the integer lattice, i.e. we identify $v_0$ with $\alpha(v_0)$ . and suppose $C_B$ is a random cluster containing $v_0$ on the Bethe lattice, and $C_Z$ is a random cluster containing $v_0$ on the integer lattice. (We are, of course, using the same value $p < 1 / (2d - 1)$ for both lattices, and considering only finite clusters.) Then we claim that for any finite collection of points $C$ , we have:

$P(C \subset C_Z) \leq P(C \subset \alpha(C_B)).$

For simplicity suppose $C$ consists of a single point $v \neq v_0$ . If $v \in C_Z$ , then there exists a non self-intersecting path from $v_0$ to $v$ that passes through points in $C_Z$ . Let us make a list of all finite non self-intersecting path $A_1, A_2, \ldots$ that go from $v_0$ to $v$ . Then $v \in C_Z$ if and only if at least one of the $A_i \subset C_Z$ .

To compute this, we add up $P(A_i \subset C_Z)$ over all of the $A_i$ , and then remove the probability that at least two of the paths are in $C_Z$ , etc. Each $P(A_i \subset C_Z)$ is easy to compute, because it is just $p^{|A_i|}$ where $|A_i|$ is the length of $A_i$ . Note that these events $A_i \subset C_Z$ are not independet of each other because some of the paths pass through the same points as other paths.

To compute $P(v \in \alpha(C_B))$ , we do exactly the same process involving adding up the $P(A_i \subset \alpha(C_B))$ . Because $\alpha$ is a covering map, each path $A_i$ has a unique preimage $\alpha^{-1}(A_i)$ on the Bethe lattice that is also a path. Thus we can do this adding up process on the Bethe lattice, and add up the $P(\alpha^{-1}(A_i) \subset C_B)$ and subtract duplicates, etc.

Certainly

$P(A_i \subset C_Z) = p^{|A_i|} = P(\alpha^{-1}(A_i) \subset C_B)$

because the paths $A_i$ and $\alpha^{-1}(A_i)$ have the same length, and we are using the same probability $p$ on both lattices.

However the joint probabilities of the paths are not the same, because there are paths that pass through the same points on the integer lattice but do not intersect on the Bethe lattice. (E.g. “right, up, up” and “up, right, right”; or indeed all of the $A_i$ end at the same point on the integer lattice but different points on the Bethe lattice.) The events $A_i \subset C_Z$ are more correlated with each other than the events $\alpha^{-1}(A_i) \subset C_B$ , so the probability that at least one event happens is greater for the latter than the former. That is, $P(v \in \alpha(C_B)) > P(v \in C_Z)$ .

Similarly this holds if $C$ is any finite collection of points, not just one point.

It follows that for any integer $m$ ,

$P(|C_Z| \geq m) \leq P(|\alpha(C_B)| \geq m) \leq P(|C_B| \geq m)$

where we have used that $|C_B| \geq |\alpha(C_B)|$ .

Since we previously saw that when $p < 1 / (z - 1)$ (the critical point on the Bethe lattice, where $z = 2d$ here), the tail probability distribution of the $|C_B|$ is exponential (i.e. $\log P(|C_B| \geq m) \sim -m$ ), it follows that $|C_Z|$ is bounded from above by an exponential.

What about bounded from below? That is easy: the $d$ dimensional integer lattice contains the 1D lattice as a subset, and so the size distribution is bounded from below by the distribution on the 1D lattice, which is also exponential. Therefore $\log P(|C_z| \geq m) \sim -m$ for large $m$ .

Now let us jump back to our earlier claim, that if we have $n$ iid randomly generated clusters, and $X_1 = |C_z|$ is the size of one of them, and $x_0$ is the median of the size of the largest one, then

$P(X_1 > x_0) \approx \frac {\log 2}{n}$

so therefore

$-x_0 \sim \log P(X_1 > x_0) \sim -\log n \sim -\log L$

and we have demonstrated the desired scaling law $x_0 \sim \log L$ (recall $n \sim L^d$ ).

While this “proof” is certainly quite hand-wavey, it is largely sound but for one critical weakness: the critical points of the Bethe lattice and integer lattice are different. This argument is only valid for $p < 1 / (2d - 1)$ , the former critical point. For $1 / (2d - 1) < p < p_c$ a more sophisticated argument is needed. This kind of approximation process, where we replace the integer lattice with an easier lattice, will never be able to bring us all the way to $p_c$ because the easier lattice has a lower critical threshold. To write a proof that is valid for all $p < p_c$ requires somehow exploiting the critical behavior as the value of $p_c$ is, in general, not definable analytically.

The fractal scaling $L^D$ is just one of many power laws that describe the behavior of a percolating cluster at or near the critical point. The exponents of these power laws are referred to as “universal” critical exponents because their value does not depend on the local shape of the grid being used as a substrate, but only on the grid’s dimension; thus all two-dimensional grids follow the same power laws. For $d \geq 6$ , the exponents stop depending on the dimension, and equal the values according to mean-field theory. Generally speaking we only have exact results for $d = 2$ , where conformal field theory can be used, or $d \geq 6$ where mean-field theory is correct.↩︎
i.e., cluster sizes distributed like a power law, and therefore $C_1$ would be a power law in $L$ ↩︎
eg “Sharpness of the Phase Transition in Percolation Models” by Michael Aizenman and David J. Barsky↩︎
Specifically, we use a power law where $q_1$ is at least 80% of $q_1$ at $p_c$ for that $L$ , and $\log L$ where $q_1$ is at most 20% of $q_1$ at $p_c$ for that $L$ .↩︎
Though from the exponent we see $C_2$ is in fact slightly catching up on $C_1$ ↩︎
necessarily, as uniform convergence of continuous functions always gives a continuous function↩︎
More rigorously, how much more likely are they to be in the same cluster than two far-away points are in the same cluster? This is the same question when $p < p_c$ , but for $p \geq p_c$ two distant points have a nonzero chance of lying in the same cluster because there is an infinite cluster. Thus what we are really asking is the chance two sites lie in the same finite cluster.↩︎
or a suitable power thereof↩︎
The distance from the origin represents the number of sites adjacent to the incomplete cluster that have not yet been determined whether they are occupied or not.↩︎
Note that if some collection $C_B$ of points in the Bethe lattice are connected, then $\alpha(C_B)$ is also connected, because $\alpha$ is a covering map and therefore sends paths to paths.↩︎
As a slight abuse of notation we will use $v_0$ to mean the origin of both the Bethe lattice and the integer lattice, i.e. we identify $v_0$ with $\alpha(v_0)$ .↩︎

Follow RSS/Atom feed for updates.